题目内容
已知函数 ,其中a,b∈R.
,其中a,b∈R.(Ⅰ)若曲线y=f(x)在点P(2,f(2))处的切线方程为y=3x+1,求函数f(x)的解析式;
(Ⅱ)讨论函数f(x)的单调性;
(Ⅲ)若对于任意的
 ,不等式f(x)≤10在
,不等式f(x)≤10在 上恒成立,求b的取值范围.
上恒成立,求b的取值范围.
【答案】分析:(Ⅰ)根据导数的几何意义即为点的斜率,再根据f(x)在点P(2,f(2))处的切线方程为y=3x+1,解出a值;
(Ⅱ)由题意先对函数y进行求导,解出极值点,因极值点含a,需要分类讨论它的单调性;
(Ⅲ)已知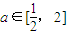 ,恒成立的问题,要根据(Ⅱ)的单调区间,求出f(x)的最大值,让f(x)的最大值小于10就可以了,从而解出b值.
,恒成立的问题,要根据(Ⅱ)的单调区间,求出f(x)的最大值,让f(x)的最大值小于10就可以了,从而解出b值.
解答:解:(Ⅰ)解: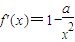 ,由导数的几何意义得f'(2)=3,于是a=-8.
,由导数的几何意义得f'(2)=3,于是a=-8.
由切点P(2,f(2))在直线y=3x+1上可得-2+b=7,解得b=9.
所以函数f(x)的解析式为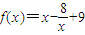 .
.
(Ⅱ)解: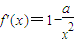 .
.
当a≤0时,显然f'(x)>0(x≠0).这时f(x)在(-∞,0),(0,+∞)上内是增函数.
当a>0时,令f'(x)=0,解得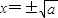 .
.
当x变化时,f'(x),f(x)的变化情况如下表:
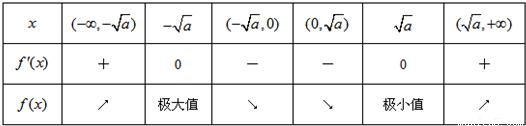
所以f(x)在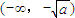 ,
,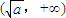 内是增函数,在
内是增函数,在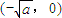 ,(0,+∞)内是减函数.
,(0,+∞)内是减函数.
(Ⅲ)解:由(Ⅱ)知,f(x)在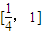 上的最大值为
上的最大值为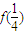 与f(1)的较大者,对于任意的
与f(1)的较大者,对于任意的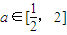 ,不等式f(x)≤10在
,不等式f(x)≤10在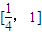 上恒成立,当且仅当
上恒成立,当且仅当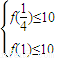 ,
,
即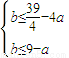 ,对任意的
,对任意的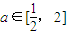 成立.
成立.
从而得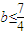 ,所以满足条件的b的取值范围是
,所以满足条件的b的取值范围是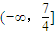 .
.
点评:本小题主要考查导数的几何意义、利用导数研究函数的单调性、解不等式等基础知识,考查运算能力、综合分析和解决问题的能力.
(Ⅱ)由题意先对函数y进行求导,解出极值点,因极值点含a,需要分类讨论它的单调性;
(Ⅲ)已知
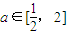 ,恒成立的问题,要根据(Ⅱ)的单调区间,求出f(x)的最大值,让f(x)的最大值小于10就可以了,从而解出b值.
,恒成立的问题,要根据(Ⅱ)的单调区间,求出f(x)的最大值,让f(x)的最大值小于10就可以了,从而解出b值.解答:解:(Ⅰ)解:
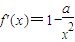 ,由导数的几何意义得f'(2)=3,于是a=-8.
,由导数的几何意义得f'(2)=3,于是a=-8.由切点P(2,f(2))在直线y=3x+1上可得-2+b=7,解得b=9.
所以函数f(x)的解析式为
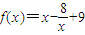 .
.(Ⅱ)解:
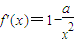 .
.当a≤0时,显然f'(x)>0(x≠0).这时f(x)在(-∞,0),(0,+∞)上内是增函数.
当a>0时,令f'(x)=0,解得
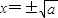 .
.当x变化时,f'(x),f(x)的变化情况如下表:

所以f(x)在
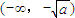 ,
,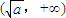 内是增函数,在
内是增函数,在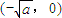 ,(0,+∞)内是减函数.
,(0,+∞)内是减函数.(Ⅲ)解:由(Ⅱ)知,f(x)在
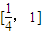 上的最大值为
上的最大值为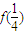 与f(1)的较大者,对于任意的
与f(1)的较大者,对于任意的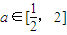 ,不等式f(x)≤10在
,不等式f(x)≤10在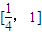 上恒成立,当且仅当
上恒成立,当且仅当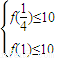 ,
,即
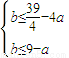 ,对任意的
,对任意的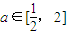 成立.
成立.从而得
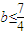 ,所以满足条件的b的取值范围是
,所以满足条件的b的取值范围是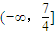 .
.点评:本小题主要考查导数的几何意义、利用导数研究函数的单调性、解不等式等基础知识,考查运算能力、综合分析和解决问题的能力.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
 ,其中a,b∈R.
,其中a,b∈R. ,不等式f(x)≤10在
,不等式f(x)≤10在 上恒成立,求b的取值范围.
上恒成立,求b的取值范围. ,其中a,b为常数.
,其中a,b为常数. (其中a,b为常数且
(其中a,b为常数且 )的反函数的图象经过点A(4,1)和B(16,3)。
)的反函数的图象经过点A(4,1)和B(16,3)。 在
在 上恒成立,求实数m的取值范围。
上恒成立,求实数m的取值范围。