题目内容
自点A(-3,3)发出的光线l射到x轴上,被x轴反射,其反射光线所在的直线与圆x2+y2-4x-4y+7=0相切,求光线l所在的直线的方程.活动:学生阅读,画出几何图形,可以多角度考虑解决问题的方法,发散思维,教师及时引导,利用待定系数法和对称的方法来解,充分考虑到直线方程的求法.
解:(待定系数法)
设光线l所在直线的方程为y-3=k(x+3),
则反射点的坐标为(![]() ,0)(k存在且k≠0).
,0)(k存在且k≠0).
∵光线的入射角等于反射角,
∴反射线l′所在直线的方程为y=-k[x+![]() ],
],
即l′:y+kx+3(1+k)=0.
∵圆(x-2)2+(y-2)2=1,l′与圆相切,
∴圆心到l′的距离d=![]() =1.
=1.
∴k=![]() k=
k=![]() .
.
∴光线l所在直线的方程为3x+4y-3=0或4x+3y+3=0.
点评:本题是方程思想的典例,方法较多,无论那种方法都是设出适当的未知数,列出相应的方程求解,对光线问题的解决,一般利用对称的方法解题,往往会收到意想不到的结果.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
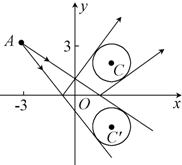 自点A(-3,3)发出的光线L射到x轴上,被x轴反射,其反射光线所在直线与圆x2+y2-4x-4y+7=0相切,求光线L所在直线的方程.
自点A(-3,3)发出的光线L射到x轴上,被x轴反射,其反射光线所在直线与圆x2+y2-4x-4y+7=0相切,求光线L所在直线的方程.