题目内容
自点A（-3，3）发出的光线L射到x轴上，被x轴反射，其反射光线所在直线与圆x2+y2-4x-4y+7=0相切，求光线L所在直线的方程
3x+4y-3=0,或4x+3y+3=0.
解析:
解：已知圆的标准方程是（x-2)2+(y-2)2=1,
它关于x轴的对称圆的方程是（x-2)2+(y+2)2=1,
设光线L所在直线的方程是y-3=k(x+3)(其中斜率k待定）
由题设知对称圆的圆心
（2，-2）到这条直线的距离等于1，即
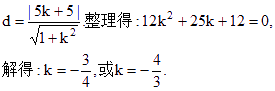
故所求的直线方程是
即3x+4y-3=0,或4x+3y+3=0.
练习册系列答案
相关题目
自点
A(－1，4)作圆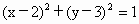
的切线，则切线长等于
[ ]
|
A ． |
B ．3 |
|
C ． |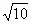
D ．5 |
的切线，则切线长等于
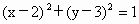的切线l，求切线l的方程．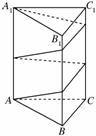
面ABC,高为5，一质点自点A出发，沿着三棱柱的侧面绕行两周到达点A1的最短路线的长为_______