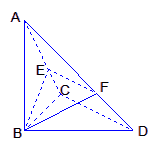
题目内容
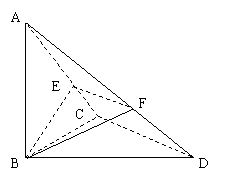 已知
已知![]() 中,
中,![]() ,
,![]() ,
,![]() ⊥平面
⊥平面![]() ,
,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的动点,且
上的动点,且![]() .
.
(1)求证不论![]() 为何值,总有平面
为何值,总有平面![]() ⊥平面
⊥平面![]() ;
;
(2)若平面![]() 与平面
与平面![]() 所成的二面角的大小为
所成的二面角的大小为![]() ,求
,求![]() 的值。
的值。
解析(1)∵![]() ⊥平面
⊥平面![]() ,∴
,∴![]() ,又在
,又在![]() 中,
中,![]() ,∴
,∴![]() ,又
,又![]() ,∴
,∴![]() ⊥平面
⊥平面![]() ,又在
,又在![]() 中
中![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的动点,且
上的动点,且![]() ,∴
,∴![]() ,∴
,∴![]() ⊥平面
⊥平面![]() ,又
,又![]() 平面
平面![]() ,∴不论
,∴不论![]() 为何值,总有平面
为何值,总有平面![]() ⊥平面
⊥平面![]() ;
;
 (2)过点
(2)过点![]() 作
作![]() ,∵
,∵![]() ⊥平面
⊥平面![]() ,∴
,∴![]() ⊥平面
⊥平面![]() ,又在
,又在![]() 中,
中,![]() ,∴
,∴![]() ,如图,以
,如图,以![]() 为原点,建立空间直角坐标系
为原点,建立空间直角坐标系![]() .又在
.又在![]() 中,
中,![]() ,
,![]() ,∴
,∴![]() 。又在
。又在![]() 中,
中,![]() ,∴
,∴![]() ,则
,则![]() 。
。
∵![]() ,∴
,∴![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
又∵![]() ,
,![]() ,
,
设![]() 是平面
是平面![]() 的法向量,则
的法向量,则![]() ,因为
,因为![]() ,所以
,所以![]() ,因为
,因为![]() =(0,1,0),所以
=(0,1,0),所以 ,令
,令![]() 得
得![]() ,
,![]() ,因为
,因为 ![]() 是平面
是平面![]() 的法向量,且平面
的法向量,且平面![]() 与平面
与平面![]() 所成的二面角为
所成的二面角为![]() ,
, ,∴
,∴![]() ,∴
,∴![]() 或
或![]() (不合题意,舍去),故当平面
(不合题意,舍去),故当平面![]() 与平面
与平面![]() 所成的二面角的大小为
所成的二面角的大小为![]() 时
时![]() 。
。

练习册系列答案
相关题目
 如图,正方体ABCD-A1B1C1D1中,E,F分别为棱DD1,AB上的点.已知下列判断:
如图,正方体ABCD-A1B1C1D1中,E,F分别为棱DD1,AB上的点.已知下列判断: