题目内容
已知,函数f(x)=2sinωx在[0, ]上递增,且在这个区间上的最大值是
]上递增,且在这个区间上的最大值是 ,那么ω等于
,那么ω等于
- A.

- B.
 或
或
- C.

- D.

D
分析:由题意根据函数的单调性,通过函数的最值,求出ω的值.
解答:因为函数f(x)=2sinωx在[0, ]上递增,且在这个区间上的最大值是
]上递增,且在这个区间上的最大值是 ,
,
所以函数f(x)=2sinω =
= ,
,
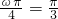 ,
,
∴ω= .
.
故选D.
点评:本题考查正弦函数的单调性,函数的值域的应用,考查计算能力.
分析:由题意根据函数的单调性,通过函数的最值,求出ω的值.
解答:因为函数f(x)=2sinωx在[0,
 ]上递增,且在这个区间上的最大值是
]上递增,且在这个区间上的最大值是 ,
,所以函数f(x)=2sinω
 =
= ,
,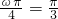 ,
,∴ω=
 .
.故选D.
点评:本题考查正弦函数的单调性,函数的值域的应用,考查计算能力.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目