Question

【题目】已知是自然对数的底数，函数与的定义域都是.

（1）求函数在点处的切线方程；

（2）判断函数零点个数;

（3）用表示的最小值，设，，若函数在上为增函数，求实数的取值范围．

Answer 1

【答案】（1）；（2）函数只有一个零点；（3）.

【解析】

（1）先求导数，代入得为直线的斜率，利用点斜式可求直线方程；

（2）先求导数，结合导数的符号，判定零点的个数；

（3）为增函数，转化为恒成立，然后利用分离参数法求解.

（1）∵，∴切线的斜率，.

∴函数在点处的切线方程为.

（2）∵，，∴，，，

∴存在零点，且.∵，

∴当时，；当时，由得

.∴在上是减函数.

∴若，，，则.∴函数只有一个零点，且.

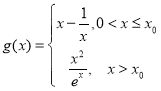（3）解：，故，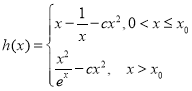

∵函数只有一个零点，∴，即.∴.

∴在为增函数在，恒成立.

当时，即在区间上恒成立.

设，只需，

，在单调递减，在单调递增.

的最小值，.

当时，，由上述得，则在恒成立.

综上述，实数的取值范围是.