题目内容
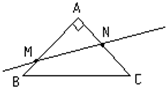 如图,△ABC是斜边为2的等腰直角三角形,点M,N分别为AB、AC上的点,过M、N的直线l将该三角形分成周长相等的两部分.
如图,△ABC是斜边为2的等腰直角三角形,点M,N分别为AB、AC上的点,过M、N的直线l将该三角形分成周长相等的两部分.(1)问AM+AN是否为定值?请说明理由.
(2)如何设计,方能使四边形BMNC的面积最小?
分析:(1)先求出腰长,然后根据过MN的直线将该三角形分成周长相等的两个部分可求出AM+AN的值;
(2)当△AMN面积最大时,四边形BMNC面积最小,利用二次函数的性质求出S△AMN有最大值,从而求出何时四边形BMNC面积最小.
(2)当△AMN面积最大时,四边形BMNC面积最小,利用二次函数的性质求出S△AMN有最大值,从而求出何时四边形BMNC面积最小.
解答:解:(1)△ABC是斜边为2的等腰直角三角形
∴AB=AC=
=
∵M N分别为AB AC 上的点,过MN的直线将该三角形分成周长相等的两个部分
∴AM+AN+MN=MB+BC+NC+MN
∴AM+AN=MB+BC+NC
又(AM+AN)+(MB+BC+NC)=AM+MB+BC+AN+NC=AB+BC+AC=2+2
∴AM+AN=MB+BC+NC=
+1
∴AM+AN为定值
(2)当△AMN面积最大时,四边形BMNC面积最小
AM+AN=
+1
令AM=x,则AN=
+1-x
S△AMN=
AM×AN=
x(
+1-x)=-
[x2-(
+1)x]
当x=
时,S△AMN有最大值,四边形BMNC面积最小
即当AM=AN=
时,四边形BMNC面积最小
∴AB=AC=
| BC | ||
|
| 2 |
∵M N分别为AB AC 上的点,过MN的直线将该三角形分成周长相等的两个部分
∴AM+AN+MN=MB+BC+NC+MN
∴AM+AN=MB+BC+NC
又(AM+AN)+(MB+BC+NC)=AM+MB+BC+AN+NC=AB+BC+AC=2+2
| 2 |
∴AM+AN=MB+BC+NC=
| 2 |
∴AM+AN为定值
(2)当△AMN面积最大时,四边形BMNC面积最小
AM+AN=
| 2 |
令AM=x,则AN=
| 2 |
S△AMN=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
当x=
| ||
| 2 |
即当AM=AN=
| ||
| 2 |
点评:本题主要考查了二次函数的最值,同时考查了计算能力和分析能力,以及转化的思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,D是直角△ABC斜边BC上一点,AB=AD,记∠CAD=a,∠ABC=β.
如图,D是直角△ABC斜边BC上一点,AB=AD,记∠CAD=a,∠ABC=β.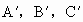 ,如果△
,如果△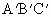 是正三角形,且
是正三角形,且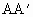 =3cm,
=3cm,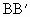 =5cm,
=5cm,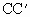 =4cm,则△
=4cm,则△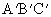 的面积是_______.
的面积是_______.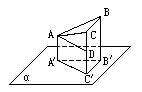
 如图,△ABC是斜边为2的等腰直角三角形,点M,N分别为AB、AC上的点,过M、N的直线l将该三角形分成周长相等的两部分.
如图,△ABC是斜边为2的等腰直角三角形,点M,N分别为AB、AC上的点,过M、N的直线l将该三角形分成周长相等的两部分.