题目内容
若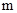 是2和8的等比中项,则圆锥曲线
是2和8的等比中项,则圆锥曲线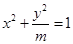 的离心率是( )
的离心率是( )
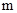 是2和8的等比中项,则圆锥曲线
是2和8的等比中项,则圆锥曲线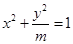 的离心率是( )
的离心率是( )A.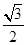 | B.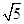 | C.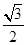 或 或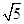 | D. |
C
试题分析:
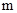 是2和8的等比中项,所以
是2和8的等比中项,所以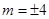 .当
.当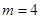 时,圆锥曲线
时,圆锥曲线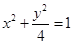 ,表示焦点在
,表示焦点在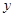 轴上的椭圆,其中
轴上的椭圆,其中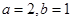 ,所以
,所以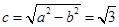 .离心率
.离心率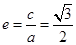 ;当
;当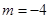 时,圆锥曲线
时,圆锥曲线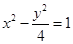 ,表示焦点在
,表示焦点在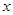 轴上的双曲线,其中
轴上的双曲线,其中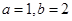 ,所以
,所以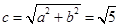 .离心率
.离心率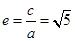 .所以离心率为
.所以离心率为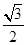 或
或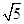 .
.
练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
题目内容
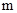 是2和8的等比中项,则圆锥曲线
是2和8的等比中项,则圆锥曲线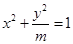 的离心率是( )
的离心率是( )A.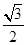 | B.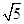 | C.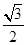 或 或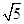 | D. |
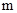 是2和8的等比中项,所以
是2和8的等比中项,所以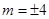 .当
.当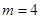 时,圆锥曲线
时,圆锥曲线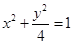 ,表示焦点在
,表示焦点在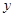 轴上的椭圆,其中
轴上的椭圆,其中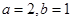 ,所以
,所以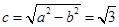 .离心率
.离心率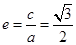 ;当
;当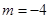 时,圆锥曲线
时,圆锥曲线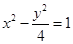 ,表示焦点在
,表示焦点在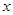 轴上的双曲线,其中
轴上的双曲线,其中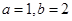 ,所以
,所以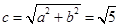 .离心率
.离心率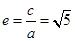 .所以离心率为
.所以离心率为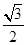 或
或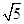 .
.
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案