题目内容
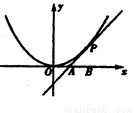
如图,已知直线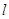 与抛物线
与抛物线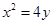 相切于点
相切于点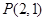 )且与
)且与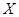 轴交于点
轴交于点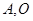 为坐标原点,定点B的坐标为
为坐标原点,定点B的坐标为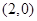 .
.
(1)若动点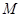 满足
满足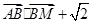 |
|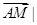 =
= ,求点
,求点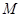 的轨迹
的轨迹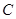 .
.
(2)若过点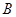 的直线
的直线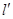 (斜率不等于零)与(1)中的轨迹
(斜率不等于零)与(1)中的轨迹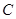 交于不同的两点
交于不同的两点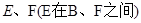 ,试求
,试求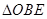 与
与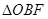 面积之比的取值范围.
面积之比的取值范围.
【答案】
(1)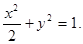 (2)
(2)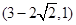
【解析】
试题分析:解:(I)由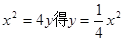 ,
,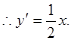
∴直线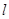 的斜率为
的斜率为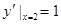 ,
,
故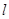 的方程为
的方程为 ,∴点A坐标为(1,0)
,∴点A坐标为(1,0)
设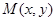 则
则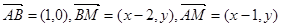 ,
,
由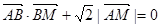 得
得 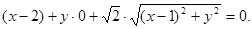
整理,得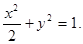
∴动点M的轨迹C为以原点为中心,焦点在x轴上,长轴长为 ,短轴长为2
,短轴长为2
的椭圆.
(II)如图,由题意知直线 的斜率存在且不为零,
的斜率存在且不为零,
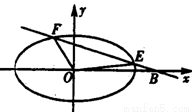
设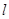 方程为y=k(x-2)(k≠0)①
方程为y=k(x-2)(k≠0)①
将①代入 ,整理,得
,整理,得
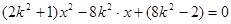 ,
,
由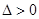 得
得 . 设
. 设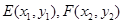
则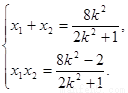 ②
②
令 ,由此可得
,由此可得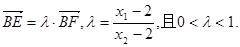
由②知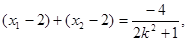
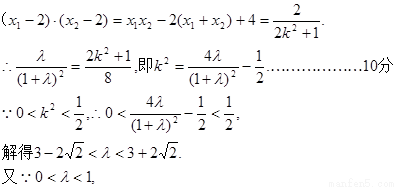
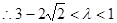
.∴△OBE与△OBF面积之比的取值范围是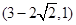 .
.
考点:椭圆的方程
点评:关于曲线的大题,第一问一般是求出曲线的方程,第二问常与直线结合起来,当涉及到交点时,常用到根与系数的关系式: (
( )。
)。

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
22.(本题满分15分)已知抛物线C的顶点在原点,焦点在y轴正半轴上,点 到其准线的距离等于5.
到其准线的距离等于5.
(Ⅰ)求抛物线C的方程;
(Ⅱ)如图,过抛物线C的焦点的直线从左到右依次与抛物线C及圆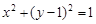 交于A、C、D、B四点,试证明
交于A、C、D、B四点,试证明 为定值;
为定值;
|
 且
且 交于点M,求
交于点M,求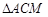 与
与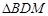 面积之和的最小值.
面积之和的最小值.
(本小题满分15分)
已知抛物线G的顶点在原点,焦点在y轴正半轴上,点P(m,4)到其准线的距离等于5。
(I)求抛物线G的方程;
(II)如图,过抛物线G的焦点的直线依次与抛物线G及圆![]() 交于A、C、D、B四点,试证明
交于A、C、D、B四点,试证明![]() 为定值;
为定值;
|
 已知抛物线G的顶点在原点,焦点在y轴正半轴上,点P(m,4)到其准线的距离等于5.
已知抛物线G的顶点在原点,焦点在y轴正半轴上,点P(m,4)到其准线的距离等于5.
 到其准线的距离等于5.
到其准线的距离等于5. 交于A、C、D、B四点,试证明
交于A、C、D、B四点,试证明 为定值;
为定值; 且
且 与
与 面积之和的最小值.
面积之和的最小值.
 |BD|为定值;
|BD|为定值;
