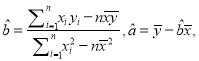题目内容
【题目】已知中心在原点的椭圆C的左焦点F（﹣ 
，0），右顶点A（2，0）．
（1）求椭圆C的标准方程；
（2）斜率为 
的直线l与椭圆C交于A、B两点，求弦长|AB|的最大值及此时l的直线方程．
【答案】
（1）解：由题意可知：c= 
，a=2，∴b2=a2﹣c2=1．
∵焦点在x轴上，
∴椭圆C的方程为： 
（2）解：设直线l的方程为y= 
x+b，由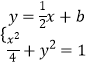 
，
可得x2+2bx+2b2﹣2=0，
∵l与椭圆C交于A、B两点，
∴△=4b2﹣4（2b2﹣2）≥0，即b2≤2．
设A（x1，y1），B（x2，y2），
则x1+x2=﹣2b，x1x2=2b2﹣2．
∴弦长|AB|= 
= 
，
∵0≤b2≤2，
∴|AB|= ≤ 
，
∴当b=0，即l的直线方程为y= x时，弦长|AB|的最大值为
【解析】（1）由已知根据椭圆的简单性质可求出a、b的值进而得到椭圆的方程。（2）联立直线和椭圆的方程得到关于x的一元二次方程，设出A、B两点的坐标根据韦达定理得到x1+x2和x1x2 关系式，代入弦长公式即可求出结果，利用椭圆自身的范围限制得到b的取值范围，进而得到弦长|AB|的最大值以及直线的方程。
【考点精析】认真审题，首先需要了解椭圆的标准方程(椭圆标准方程焦点在x轴：
，焦点在y轴：
)．
练习册系列答案
相关题目
