题目内容
已知函数f(x)=x2+3x,数列{an}的前n项和为Sn,且对一切正整数n,点Pn(n,Sn)都在函数f(x)的图象上.
(1)求数列{an}的通项公式;
(2)设A={x|x=an,n∈N*},B={x|x=2(an-1),n∈N*},等差数列{bn}的任一项bn∈A∩B,其中b1是A∩B中最的小数,且88<b8<93,求{bn}的通项公式;
(3)设数列{cn}满足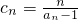 ,是否存在正整数p,q(1<p<q),使得c1,cp,cq成等比数列?若存在,求出所有的p,q的值;若不存在,请说明理由.
,是否存在正整数p,q(1<p<q),使得c1,cp,cq成等比数列?若存在,求出所有的p,q的值;若不存在,请说明理由.
解:(1)∵点Pn(n,Sn)都在函数f(x)=x2+3x的图象上,∴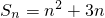 .
.
当n=1时,a1=S1=4;
当n≥2时,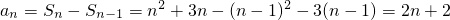 ,
,
当n=1时,也满足.
故an=2n+2.
(2)∵A={x|x=an,n∈N*},B={x|x=2(an-1),n∈N*},
∴A={x|x=2n+2,n∈N*},B={x|x=4n+2,n∈N*}
∴A∩B=B,
又∵bn∈A∩B,∴bn∈B即数列{bn}的公差是4 的倍数
又A∩B中的最小数为6,∴b1=6,∴b8=4k+6,k∈N*,
又∵88<b8<93
∴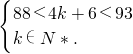 ,解得k=21.
,解得k=21.
等差数列{bn}的公差为d,由b8=6+7d=90得d=12,故bn=12n-6
(3)∵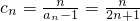 ,∴
,∴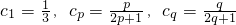
若c1,cp,cq成等比数列,则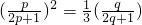 ,即
,即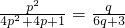 .
.
可得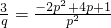 ,所以-2p2+4p+1>0,
,所以-2p2+4p+1>0,
从而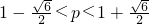
又p∈N*,∴p=2,此时q=12.
故当且仅当p=2,q=12,使得c1,cp,cq成等比数列.
分析:(1)利用点Pn(n,Sn)都在函数f(x)=x2+3x的图象上,可得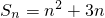 ,再写一式,两式相减,即可求得数列{an}的通项公式;
,再写一式,两式相减,即可求得数列{an}的通项公式;
(2)先确定A∩B=B,进而可得数列{bn}的公差是4 的倍数,利用b1是A∩B中最的小数,且88<b8<93,即可求{bn}的通项公式;
(3)利用c1,cp,cq成等比数列,建立方程,可求正整数p,q的值.
点评:本题考查数列的通项,考查等比数列的性质,考查数列与函数的联系,考查学生分析解决问题的能力,正确确定数列的通项是关键.
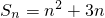 .
.当n=1时,a1=S1=4;
当n≥2时,
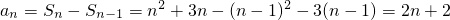 ,
,当n=1时,也满足.
故an=2n+2.
(2)∵A={x|x=an,n∈N*},B={x|x=2(an-1),n∈N*},
∴A={x|x=2n+2,n∈N*},B={x|x=4n+2,n∈N*}
∴A∩B=B,
又∵bn∈A∩B,∴bn∈B即数列{bn}的公差是4 的倍数
又A∩B中的最小数为6,∴b1=6,∴b8=4k+6,k∈N*,
又∵88<b8<93
∴
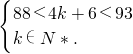 ,解得k=21.
,解得k=21. 等差数列{bn}的公差为d,由b8=6+7d=90得d=12,故bn=12n-6
(3)∵
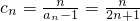 ,∴
,∴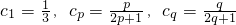
若c1,cp,cq成等比数列,则
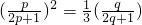 ,即
,即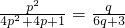 .
. 可得
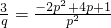 ,所以-2p2+4p+1>0,
,所以-2p2+4p+1>0,从而
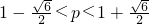
又p∈N*,∴p=2,此时q=12.
故当且仅当p=2,q=12,使得c1,cp,cq成等比数列.
分析:(1)利用点Pn(n,Sn)都在函数f(x)=x2+3x的图象上,可得
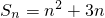 ,再写一式,两式相减,即可求得数列{an}的通项公式;
,再写一式,两式相减,即可求得数列{an}的通项公式; (2)先确定A∩B=B,进而可得数列{bn}的公差是4 的倍数,利用b1是A∩B中最的小数,且88<b8<93,即可求{bn}的通项公式;
(3)利用c1,cp,cq成等比数列,建立方程,可求正整数p,q的值.
点评:本题考查数列的通项,考查等比数列的性质,考查数列与函数的联系,考查学生分析解决问题的能力,正确确定数列的通项是关键.

练习册系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|