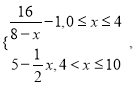题目内容
【题目】在直角坐标系xOy中,曲线C1: ![]() (t为参数,t≠0),其中0≤α<π.在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=2sin θ,C3:ρ=2
(t为参数,t≠0),其中0≤α<π.在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=2sin θ,C3:ρ=2![]() cos θ.
cos θ.
(1)求C2与C3交点的直角坐标;
(2)若C1与C2相交于点A,C1与C3相交于点B,求|AB|的最大值.
【答案】(1)(0,0)和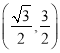 .(2)4.
.(2)4.
【解析】试题分析:(1)将![]() 与
与![]() 转化为直角坐标方程,解方程组即可求出交点坐标;(2)求出
转化为直角坐标方程,解方程组即可求出交点坐标;(2)求出![]() ,
, ![]() 的极坐标,利用距离公式进行求解.
的极坐标,利用距离公式进行求解.
试题解析:(1)曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ,
,
曲线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
联立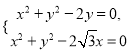 解得
解得![]() 或
或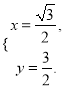
所以![]() 与
与![]() 交点的直角坐标为
交点的直角坐标为![]() 和
和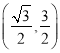
(2)曲线![]() 的极坐标方程为
的极坐标方程为![]() ,其中
,其中![]()
因此![]() 的极坐标为
的极坐标为![]() ,
, ![]() 的极坐标为[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2016/6/1/1572680658870272/1572680665268224/EXPLANATION/e9b48f59939d4f508c427ac0fd6678ec.png]
的极坐标为[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2016/6/1/1572680658870272/1572680665268224/EXPLANATION/e9b48f59939d4f508c427ac0fd6678ec.png]
所以![]()
当![]() 时,
时, ![]() 取得最大值,最大值为4
取得最大值,最大值为4

【题目】为了治理大气污染,某市2017年初采用了一系列措施,比如“煤改电”,“煤改气”,“国Ⅰ,Ⅱ轻型汽油车限行”,“整治散乱污染企业”等.下表是该市2016年和2017年12月份的空气质量指数(AQI)(AQI指数越小,空气质量越好)统计表.
表1:2016年12月AQI指数表:单位(![]() )
)
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
AQI | 47 | 123 | 232 | 291 | 78 | 103 | 159 | 132 | 37 | 67 | 204 |
日期 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
AQI | 270 | 78 | 40 | 51 | 135 | 229 | 270 | 265 | 409 | 429 | 151 |
日期 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | ||
AQI | 47 | 155 | 191 | 64 | 54 | 85 | 75 | 249 | 329 |
表2:2017年12月AQI指数表:单位(![]() )
)
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
AQI | 91 | 187 | 79 | 28 | 44 | 49 | 27 | 41 | 56 | 43 | 28 |
日期 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
AQI | 28 | 49 | 94 | 62 | 40 | 46 | 48 | 55 | 44 | 74 | 62 |
日期 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | ||
AQI | 50 | 50 | 46 | 41 | 101 | 140 | 221 | 157 | 55 |
根据表中数据回答下列问题:
(Ⅰ)求出2017年12月的空气质量指数的极差;
(Ⅱ)根据《环境空气质量指数(AQI)技术规定(试行)》规定:当空气质量指数为0~50时,空气质量级别为一级.从2017年12月12日到12月16这五天中,随机抽取三天,空气质量级别为一级的天数为![]() ,求
,求![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅲ)你认为该市2017年初开始采取的这些大气污染治理措施是否有效?结合数据说明理由.
【题目】某次有600人参加的数学测试,其成绩的频数分布表如图所示,规定85分及其以上为优秀.
区间 | [75,80) | [80,85) | [85,90) | [90,95) | [95,100] |
人数 | 36 | 114 | 244 | 156 | 50 |
(Ⅰ)现用分层抽样的方法从这600人中抽取20人进行成绩分析,求其中成绩为优秀的学生人数;
(Ⅱ)在(Ⅰ)中抽取的20名学生中,要随机选取2名学生参加活动,记“其中成绩为优秀的人数”为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.