题目内容
函数f(x)=x-2lnx在(0,2]上的值域为________.
[2-2ln2,+∞)
分析:由题意得f′(x)=1- =
=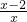 分析得到函数f(x)=x-2lnx在(0,2]上是减函数,所以当x=2时函数f(x)有最小值2-2ln2,当x趋向于0时函数值趋向于+∞.
分析得到函数f(x)=x-2lnx在(0,2]上是减函数,所以当x=2时函数f(x)有最小值2-2ln2,当x趋向于0时函数值趋向于+∞.
解答:由题意得f′(x)=1- =
=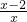
因为x∈(0,2]
所以f′(x)<0
所以函数f(x)=x-2lnx在(0,2]上是减函数.
所以当x=2时函数f(x)有最小值2-2ln2,当x趋向于0时函数值趋向于+∞.
所以函数f(x)=x-2lnx在(0,2]上的值域为[2-2ln2,+∞).
故答案为:[2-2ln2,+∞).
点评:解决此类问题关键是正确求函数的导数并且分析导数的符号判断出原函数的单调性,进而求出函数的最值得出函数的值域.
分析:由题意得f′(x)=1-
 =
=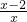 分析得到函数f(x)=x-2lnx在(0,2]上是减函数,所以当x=2时函数f(x)有最小值2-2ln2,当x趋向于0时函数值趋向于+∞.
分析得到函数f(x)=x-2lnx在(0,2]上是减函数,所以当x=2时函数f(x)有最小值2-2ln2,当x趋向于0时函数值趋向于+∞.解答:由题意得f′(x)=1-
 =
=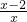
因为x∈(0,2]
所以f′(x)<0
所以函数f(x)=x-2lnx在(0,2]上是减函数.
所以当x=2时函数f(x)有最小值2-2ln2,当x趋向于0时函数值趋向于+∞.
所以函数f(x)=x-2lnx在(0,2]上的值域为[2-2ln2,+∞).
故答案为:[2-2ln2,+∞).
点评:解决此类问题关键是正确求函数的导数并且分析导数的符号判断出原函数的单调性,进而求出函数的最值得出函数的值域.

练习册系列答案
相关题目