题目内容
有下列四个命题:
①
与
的夹角为锐角的充要条件是
•
>0.
②?x,y∈R,sin(x-y)=sinx-siny;
③?a∈(0,1)∪(1,+∞),函数f(x)=a1-2x+1都恒过定点(
,2);
④方程x2+y2+Dx+Ey+F=0表示圆的充要条件是D2+E2-4F≥0;
其中正确命题的序号是
①
| a |
| b |
| a |
| b |
②?x,y∈R,sin(x-y)=sinx-siny;
③?a∈(0,1)∪(1,+∞),函数f(x)=a1-2x+1都恒过定点(
| 1 |
| 2 |
④方程x2+y2+Dx+Ey+F=0表示圆的充要条件是D2+E2-4F≥0;
其中正确命题的序号是
②③
②③
.(将正确命题的序号都填上)分析:①若非零向量
与
的夹角为锐角,则一定有
•
>0,;反之,满足
•
>0的
与
同向共线时,其
与
夹角为0°,却不是锐角,故可以判断①真假.
②取x=y=0时,可以判断出②的真假.
③当x=
时,其函数值f(
)=2与a无关,故可以判断函数f(x)=a1-2x+1都恒过定点(
,2),由此可以判断③真假.
④方程x2+y2+Dx+Ey+F=0经配方可化为:(x+
)2+(y+
)2=
,有此式可以判断出方程x2+y2+Dx+Ey+F=0何时表示圆,进而可知④的真假.
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
②取x=y=0时,可以判断出②的真假.
③当x=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
④方程x2+y2+Dx+Ey+F=0经配方可化为:(x+
| D |
| 2 |
| E |
| 2 |
| D2+E2-4F |
| 4 |
解答:解:①若非零向量
与
的夹角为锐角,则
•
=|
||
|cos<
,
>>0;反之,当
与
同向共线时,满足
•
>0,则向量
与
夹角为0°,却不是锐角,故①是假命题.
②当x=y=0时,该等式成立,故②是真命题.
③当x=
时,f(
)=2,,故对于?a∈(0,1)∪(1,+∞),函数f(x)=a1-2x+1都恒过定点(
,2),因此③是真命题;
④方程x2+y2+Dx+Ey+F=0经配方可化为:(x+
)2+(y+
)2=
,只有当D2+E2-4F>0时,方程x2+y2+Dx+Ey+F=0才表示圆,而当D2+E2-4F=0时该方程表示点(-
,-
).故④是假命题.
故答案为②③.
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
②当x=y=0时,该等式成立,故②是真命题.
③当x=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
④方程x2+y2+Dx+Ey+F=0经配方可化为:(x+
| D |
| 2 |
| E |
| 2 |
| D2+E2-4F |
| 4 |
| D |
| 2 |
| E |
| 2 |
故答案为②③.
点评:本题主要考查向量夹角公式、全称命题与特称命题、指数函数类型的图象过定点问题、圆的一般方程何时表示圆,解决问题的关键是准确掌握有关基础知识.

练习册系列答案
相关题目
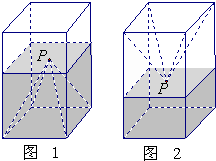 如图(1),一个正四棱柱形的密闭容器水平放置,其底部镶嵌了同底的正四棱锥形实心装饰块,容器内盛有a升水时,水面恰好经过正四棱锥的顶点P.如果将容器倒置,水面也恰好过点P(图(2))
如图(1),一个正四棱柱形的密闭容器水平放置,其底部镶嵌了同底的正四棱锥形实心装饰块,容器内盛有a升水时,水面恰好经过正四棱锥的顶点P.如果将容器倒置,水面也恰好过点P(图(2))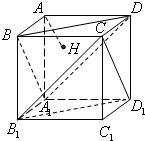 如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H.有下列四个命题:
如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H.有下列四个命题: