Question

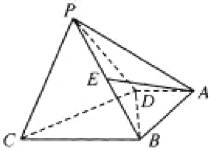
【题目】为了调查我市在校中学生参加体育运动的情况，从中随机抽取了16名男同学和14 名女同学，调查发现，男、女同学中分别有12人和6人喜爱运动，其余不喜爱.

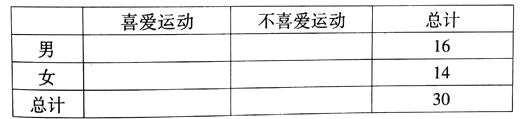
（1）根据以上数据完成以下列联表：

（2）根据列联表的独立性检验，能否在犯错误的概率不超过0.010的前提下认为性别与喜爱运动有关？

（3）将以上统计结果中的频率视作概率，从我市中学生中随机抽取3人，若其中喜爱运动的人数为，求的分布列和均值.

参考数据：

Answer 1

【答案】（1）见解析；（2）见解析；（3）见解析

【解析】分析：（1）本题是一个简单的数字的运算，根据a，b，c，d的已知和未知的结果，做出空格处的结果；（2）假设是否喜爱运动与性别无关，由已知数据可求得观测值，把求得的观测值同临界值进行比较，得到在犯错的概率不超过0.10的前提下不能判断喜爱运动与性别有关；（3）喜爱运动的人数为ξ，ξ的取值分别为0，1，2，3，结合变量对应的事件利用等可能事件的概率公式做出概率，写出分布列和期望．

详解：

（1）

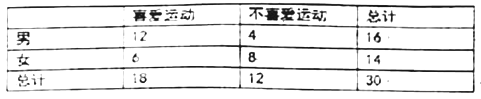
（2）假设：是否喜爱运动与性别无关，由已知数据可求得，

因此，在犯错的概率不超过0.10的前提下不能判断喜爱运动与性别有关.

（3）统计结果中喜爱运动的中学生所占的频率为.

喜爱运动的人数为的取值分别为：0,1,2,3，则有：

喜爱运动的人数为的分布列为：

因为，所以喜爱运动的人数的值为.