题目内容
若方程x2sinα-y2cosα=1(0≤α<2π)表示等轴双曲线,则角α的值为( )
分析:利用等轴双曲线的定义,可得sinα=cosα,所以tanα=1,结合0≤α<2π,可求角α的值.
解答:解:∵方程x2sinα-y2cosα=1(0≤α<2π)表示等轴双曲线
∴sinα=cosα
∴tanα=1
∵0≤α<2π
∴角α的值为
或
故选C.
∴sinα=cosα
∴tanα=1
∵0≤α<2π
∴角α的值为
| π |
| 4 |
| 5π |
| 4 |
故选C.
点评:本题以双曲线为载体,考查等轴双曲线的定义,考查三角函数,属于基础题.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
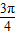 或
或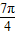
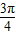 或
或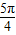
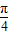 或
或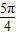
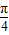 或
或