题目内容
设椭圆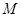 :
:
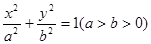 的离心率为
的离心率为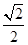 ,点
,点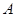 (
(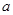 ,0),
,0),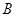 (0,
(0,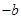 )原点
)原点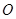 到直线
到直线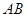 的距离为
的距离为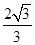 。
。
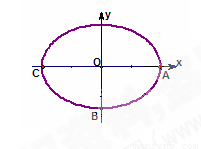
(1) 求椭圆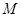 的方程;
的方程;
(2) 设点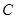 为(
为(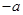 ,0),点
,0),点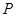 在椭圆
在椭圆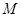 上(与
上(与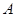 、
、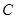 均不重合),点
均不重合),点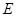 在直线
在直线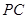 上,若直线
上,若直线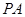 的方程为
的方程为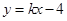 ,且
,且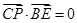 ,试求直线
,试求直线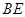 的方程.
的方程.
【答案】
(1)椭圆方程为: 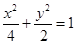 ,(2)直线
,(2)直线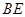 方程为
方程为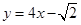
【解析】
试题分析:(1)由离心率为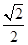 可得出
可得出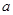 与
与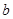 的关系,再由点
的关系,再由点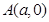 ,
,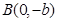 知直线
知直线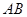 的方程,利用点到直线的距离公式可得
的方程,利用点到直线的距离公式可得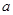 与
与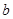 的值求出椭圆的标准方程。
的值求出椭圆的标准方程。
(2)由(1)知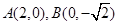 ,又因为直线
,又因为直线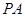 经过点
经过点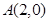 ,所以可表示出直线
,所以可表示出直线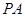 方程,进而求出
方程,进而求出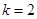 ,得出
,得出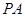 的方程又
的方程又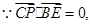
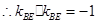 联立求解得直线
联立求解得直线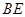 方程。
方程。
试题解析:(1)由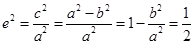
得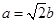
由点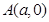 ,
,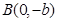 知直线
知直线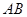 的方程为
的方程为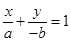
所以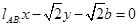 则
则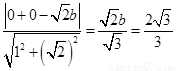
所以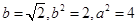 4分
4分
所以椭圆方程为: 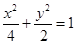 5分
5分
(2) 由(1)知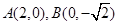 ,因为直线
,因为直线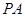 经过点
经过点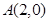 ,所以
,所以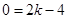
得, 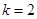 ,即直线
,即直线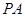 的方程为
的方程为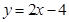 . 7分
. 7分
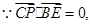
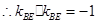 ,即
,即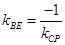 9分
9分
由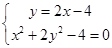 得
得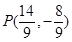 则
则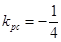 12分
12分
所以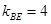 又
又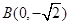 ,因此直线
,因此直线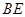 方程为
方程为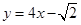 14分
14分
考点:椭圆的定义,直线与椭圆的关系,向量垂直.

练习册系列答案
相关题目
4.设椭圆C1的离心率为
,焦点在x轴上且长轴长为26,若曲线C2上的点到椭圆C1的两个焦点的距离的差的绝对值等于8,则曲线C2的标准方程为( )
| 5 |
| 13 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设椭圆C1的离心率为
,焦点在x轴上且长轴长为26,若曲线C2上的点到C1的两个焦点的距离的差的绝对值为8,则曲线C2的标准方程为( )
| 5 |
| 13 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,椭圆Ⅰ与Ⅱ有公共的左顶点和公共的左焦点F,且椭圆Ⅱ的右顶点为椭圆Ⅰ的中心,设椭圆Ⅰ与Ⅱ的离心率分别为e1和e2,则( )
如图,椭圆Ⅰ与Ⅱ有公共的左顶点和公共的左焦点F,且椭圆Ⅱ的右顶点为椭圆Ⅰ的中心,设椭圆Ⅰ与Ⅱ的离心率分别为e1和e2,则( )