题目内容
椭圆ax2+by2+ab=0(a<b<0)的焦点坐标是________.
(0,-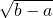 ),(0,
),(0,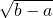 )
)
分析:将椭圆的方程ax2+by2+ab=0(a<b<0)化为标准形式,即可求得答案.
解答:椭圆的方程ax2+by2+ab=0(a<b<0)化为标准形式为: ,
,
∵a<b<0
∴-a>-b>0
∴椭圆的焦点在y轴,
∴c2=-a+b,又该椭圆焦点在y轴,
∴焦点坐标为:(0,-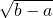 ),(0,
),(0,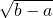 ).
).
故答案为:(0,-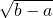 ),(0,
),(0,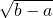 ).
).
点评:本题考查椭圆的简单性质,将椭圆的方程化为标准形式是关键,属于基础题.
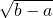 ),(0,
),(0,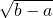 )
)分析:将椭圆的方程ax2+by2+ab=0(a<b<0)化为标准形式,即可求得答案.
解答:椭圆的方程ax2+by2+ab=0(a<b<0)化为标准形式为:
 ,
,∵a<b<0
∴-a>-b>0
∴椭圆的焦点在y轴,
∴c2=-a+b,又该椭圆焦点在y轴,
∴焦点坐标为:(0,-
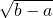 ),(0,
),(0,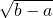 ).
).故答案为:(0,-
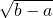 ),(0,
),(0,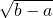 ).
).点评:本题考查椭圆的简单性质,将椭圆的方程化为标准形式是关键,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目