题目内容
(理)椭圆ax2+by2=1与直线y=-x+1交于A、B两点,过原点与线段AB中点的直线斜率为
| ||
| 2 |
| a |
| b |
分析:设A(x1,y1),B(x2,y2),则ax12+by12=1,ax22+by22=1,由此得a(x1-x2)(x1+x2)+b(y1-y2)(y1+y2)=0,由此能导出
的值.
| a |
| b |
解答:解:设A(x1,y1),B(x2,y2),
则ax12+by12=1 ①,ax22+by22=1 ②,
①-②式可得a(x1-x2)(x1+x2)+b(y1-y2)(y1+y2)=0,
从而得
=-
=-(-1)•
=
.
故答案为:
.
则ax12+by12=1 ①,ax22+by22=1 ②,
①-②式可得a(x1-x2)(x1+x2)+b(y1-y2)(y1+y2)=0,
从而得
| a |
| b |
| (y1-y2)(y1+y2) |
| (x1-x2)(x1+x2) |
| ||
| 2 |
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查了直线与椭圆的位置关系及中点弦问题的求解策略,考查了考生对“设而不求法”的掌握.

练习册系列答案
相关题目
 ,则
,则 =________.
=________.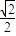 ,则
,则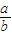 = .
= .