题目内容
已知椭圆 ,抛物线
,抛物线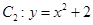 ,点
,点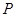 是
是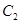 上的动点,过
上的动点,过
点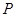 作抛物线
作抛物线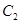 的切线
的切线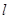 ,交椭圆
,交椭圆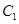 于
于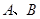 两点,
两点,
(1)当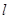 的斜率是
的斜率是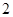 时,求
时,求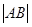 ;
;
(2)设抛物线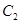 的切线方程为
的切线方程为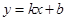 ,当
,当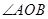 是锐角时,求
是锐角时,求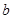 的取值范围.
的取值范围.
【答案】
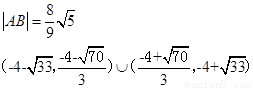
【解析】(1)根据l的斜率为2,可知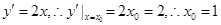 ,
,
所以P(1,3),所以直线l的方程为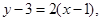 即
即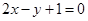 .
.
然后与椭圆方程联立借助韦达定理及弦长公式求弦长|AB|的值.
(II)设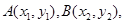
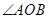 为锐角,针对本题它等价于
为锐角,针对本题它等价于 ,
,
即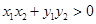 ,
,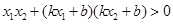 ,再根据
,再根据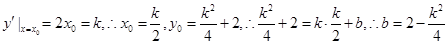 ,
,
然后直线方程与抛物线方程联立,借助韦达定理及判别式解决即可

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
已知椭圆 、抛物线
、抛物线 的焦点均在
的焦点均在 轴上,
轴上, 的中心和
的中心和 的顶点均为原点
的顶点均为原点 ,从每条曲线上取两个点,将其坐标记录于下表中:
,从每条曲线上取两个点,将其坐标记录于下表中:
|
|
3 |
|
4 |
|
|
|
|
0 |
|
|
(1)求 ,
, 的标准方程;
的标准方程;
(2)请问是否存在直线 满足条件:①过
满足条件:①过 的焦点
的焦点 ;②与
;②与 交于不同两点
交于不同两点 ,
, ,且满足
,且满足 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
已知椭圆 、抛物线
、抛物线 的焦点均在
的焦点均在 轴上,
轴上, 的中心和
的中心和 的顶点均为原点
的顶点均为原点 ,从每条曲线上取两个点,将其坐标记录于下表中:
,从每条曲线上取两个点,将其坐标记录于下表中:
|
|
3 |
|
4 |
|
|
|
|
0 |
|
|
(Ⅰ)求 的标准方程;
的标准方程;
(Ⅱ)请问是否存在直线 满足条件:①过
满足条件:①过 的焦点
的焦点 ;②与
;②与 交不同两点
交不同两点 且满足
且满足 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,说明理由。
的方程;若不存在,说明理由。






 2
2



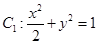 ,抛物线
,抛物线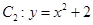 ,点
,点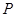 是
是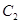 上的动点,过点
上的动点,过点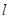 ,交椭圆
,交椭圆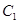 于
于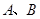 两点,
两点,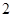 时,求
时,求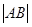 ;
;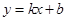 ,当
,当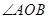 是锐角时,求
是锐角时,求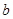 的取值范围.
的取值范围.