题目内容
下列四说法:
①不等式0.52x>0.5x-1的解集为(-1,+∞);
②已知2m=3n=36,则
+
的值为
;
③函数y=3+loga(2x+3),(a>0,a≠1)的图象恒经过的定点P的坐标为(-1,3);
④已知集合A={y|y=log2x,x>1},B={y|y=(
)x,x>1},则A∩B={y|0<y<
}.
其中正确的说法是( )
①不等式0.52x>0.5x-1的解集为(-1,+∞);
②已知2m=3n=36,则
| 1 |
| m |
| 1 |
| n |
| 1 |
| 2 |
③函数y=3+loga(2x+3),(a>0,a≠1)的图象恒经过的定点P的坐标为(-1,3);
④已知集合A={y|y=log2x,x>1},B={y|y=(
| 1 |
| 2 |
| 1 |
| 2 |
其中正确的说法是( )
| A、②③ | B、②③④ |
| C、①③④ | D、①②③④ |
分析:根据指数函数与对数函数的性质对四个结论逐一进行判断,可以得到正确的结论.
解答:解:①由0.52x>0.5x-1得2x<x-1,解得x<-1,解集不是区间形式,故①不对;
②由条件得,
=log362,
=log363,
+
=log362+log363=log366=
故②正确;
③令x=-1可得y=3故③正确;
④由y=log2x,x>1得y>0,∴A=y|y>0},由y=(
)x,x>1得0<y<
∴B={y|0<y<
},A∩B={y|0<y<
}故④正确.
综上所述,正确答案为②③④
故选B.
②由条件得,
| 1 |
| m |
| 1 |
| n |
| 1 |
| m |
| 1 |
| n |
| 1 |
| 2 |
③令x=-1可得y=3故③正确;
④由y=log2x,x>1得y>0,∴A=y|y>0},由y=(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
综上所述,正确答案为②③④
故选B.
点评:本题考查了指数函数和对数函数的一些性质,利用好对数的运算性质是判断②的关键,其它的容易判断.

练习册系列答案
相关题目
 0的解集为[2,+∞);
0的解集为[2,+∞); ”成立的必要不充分条件;
”成立的必要不充分条件; 个单位即可得到函数
个单位即可得到函数 的图象;
的图象; 的值域为R,则实数a的取值范围是(-2
的值域为R,则实数a的取值范围是(-2 ,2
,2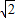 ).
). 的值为
的值为 ;
; ,则
,则 .
.