题目内容
已知实数a＞0，直线l过点P（2，-2），且垂直于向量
=(3， -3)，若直线l与圆x2+y2-2ax+a2-a=0相交，则实数a的取值范围是______．
| m |
由题意可得直线L的斜率K=1，直线l的方程为y+2=x-2即x-y-4=0
直线l与圆x2+y2-2ax+a2-a=0即（x-a）2+y2=a相交
则圆心（a，0）到直线l的距离d=
＜
解不等式可得，2＜a＜8
故答案为：2＜a＜8
直线l与圆x2+y2-2ax+a2-a=0即（x-a）2+y2=a相交
则圆心（a，0）到直线l的距离d=
| |a-4| | ||
|
| a |
解不等式可得，2＜a＜8
故答案为：2＜a＜8
练习册系列答案
相关题目
已知实数a＞0，b＜0，c＞0，则直线ax+by-c=0通过（ ）
| A、第一、二、三象限 | B、第一、二、四象限 | C、第一、三、四象限 | D、第二、三、四象限 |
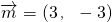，若直线l与圆x2+y2-2ax+a2-a=0相交，则实数a的取值范围是________．
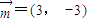，若直线l与圆x2+y2-2ax+a2-a=0相交，则实数a的取值范围是 ．