题目内容
 某空间几何体的三视图如图所示.
某空间几何体的三视图如图所示.(1)写出该几何体的结构特征,并画出该几何体的图形;
(2)求出该几何体的表面积和体积.
分析:(1)通过三视图判断几何体的形状,即可写出该几何体的结构特征,然后画出该几何体的图形;
(2)通过三视图的数据,即可求出该几何体的表面积和体积.
(2)通过三视图的数据,即可求出该几何体的表面积和体积.
解答: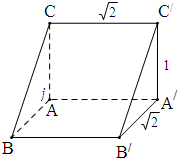 解:(1)由几何体的三视图可知,该几何体是横放的直三棱柱ABC-A'B'C',底面ABC是两直角边长分别为1和
解:(1)由几何体的三视图可知,该几何体是横放的直三棱柱ABC-A'B'C',底面ABC是两直角边长分别为1和
的直角三角形,侧棱长为
.
如图所示.
(2)因为该几何体两底面的面积和2×(
×
×1)=
,
该几何体侧面积S侧=S四边形BB'C'C+S四边形AA'C'C+S四边形ABB'A'=(
×
)+
×1+(
×
)=
+
+2
所以该几何体的表面积S表=S侧+S上底+S下底=
+2
+2,
该几何体的体积为VABC-A′B′C′=
×(
×1×
)×
=
.
 解:(1)由几何体的三视图可知,该几何体是横放的直三棱柱ABC-A'B'C',底面ABC是两直角边长分别为1和
解:(1)由几何体的三视图可知,该几何体是横放的直三棱柱ABC-A'B'C',底面ABC是两直角边长分别为1和| 2 |
| 2 |
如图所示.
(2)因为该几何体两底面的面积和2×(
| 1 |
| 2 |
| 2 |
| 2 |
该几何体侧面积S侧=S四边形BB'C'C+S四边形AA'C'C+S四边形ABB'A'=(
| 3 |
| 2 |
| 2 |
| 2 |
| 2 |
| 6 |
| 2 |
所以该几何体的表面积S表=S侧+S上底+S下底=
| 6 |
| 2 |
该几何体的体积为VABC-A′B′C′=
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 3 |
点评:本题考查三视图与几何体的结构特征,考查空间想象能力以及计算能力.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案
相关题目
 某空间几何体的三视图如图所示,求该几何体的体积.
某空间几何体的三视图如图所示,求该几何体的体积. 若某空间几何体的三视图如图所示,则该几何体的体积是( )
若某空间几何体的三视图如图所示,则该几何体的体积是( ) (2010•陕西高考理科•T7)若某空间几何体的三视图如图所示,则该几何体的体积是( )
(2010•陕西高考理科•T7)若某空间几何体的三视图如图所示,则该几何体的体积是( )