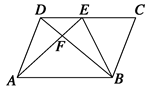
题目内容
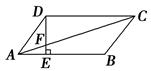
如图所示，在?ABCD中，E为CD上一点，DE∶CE＝2∶3，连接AE、BE、BD，且AE、BD交于点F，则S△DEF∶S△EBF∶S△ABF等于
| A．4∶10∶25 | B．4∶9∶25 |
| C．2∶3∶5 | D．2∶5∶25 |
A
因为AB∥CD，所以△ABF∽△EDF，
所以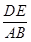
＝
＝
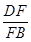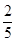，所以
＝
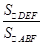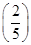2＝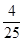
，
又△DEF、△BEF分别以DF、BF为底时等高，所以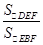
＝＝＝
.
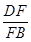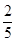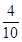故S△DEF∶S△EBF∶S△ABF＝4∶10∶25.
所以
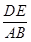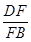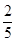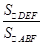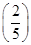＝＝，所以＝2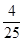＝，又△DEF、△BEF分别以DF、BF为底时等高，所以
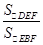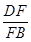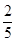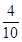＝＝＝.故S△DEF∶S△EBF∶S△ABF＝4∶10∶25.
练习册系列答案
导学与测试系列答案
新非凡教辅冲刺100分系列答案
相关题目
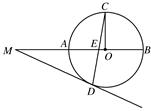
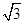，求MA及CE的长．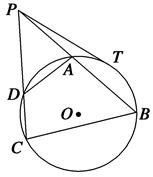
＝
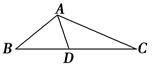
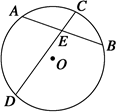
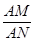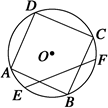
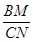，下列结论中正确的是 ( )．