题目内容
(1)
将8本练习本分给5名学生,每人至少1本,有多少种不同的分法?(2)
将n个相同的小球分别放入m个不同的盒子里(m≤n),不允许出现空盒的情况,有多少种不同的放法?
答案:略
解析:
解析:
|
解析: (1)把8本练习本排成一行,在它们之间的7个空档处(不包括左、右两端)插入4块“隔板”,使8本书分成5份,对应分给5名学生.因此,不同的插法就对应着不同分法.所以,不同的分法有 种. 种.
(2) 将n个小球排成一行,并用(m-1)块“隔板”将它们隔成m段,然后再将各段分别对应各个盒子,因此隔法的总数就是所要求出的分法的总数.因为不能出现空盒,所以“隔板”只能放在n个小球之间的间隔位置上,而且每个间隔位置只能放1块“隔板”,所以从(n-1)个间隔位置上选出(m-1)个来放置“隔板”应有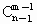 种不同的放法.也就是 种不同的放法.也就是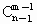 种符合要求的分球入盒方法. 种符合要求的分球入盒方法. |

练习册系列答案
相关题目
右图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图,那么甲、乙两人这几场比赛得分的中位数之和是 ( )
| 甲 |
| 乙 | ||||||
| 3 | 1 |
| ||||||
| 8 | 6 | 3 | 2 | 4 | 5 | |||
| 9 | 7 | 3 | 2 | 6 | 7 | |||
| 1 | 4 | 5 | 7 | |||||
A.65 B.64 C.63 D.62