Question

【题目】已知奇函数的定义域为.

（1）求实数，的值；

（2）判断函数的单调性，若实数满足，求的取值范围.

Answer 1

【答案】（1），（2）

【解析】试题分析：（1）根据奇函数的定义得到，即，整理得，故a=1，再根据奇函数的定义域对称求b；（2）根据单调性的定义证明即可；（3）根据函数的单调性得到关于m的不等式组，解不等式组可得所求范围。

试题解析：

（1）∵f（x）是奇函数，

∴，

即，

∴，

∴，

整理得

∴a﹣1=0，

解得：a=1，

故﹣a﹣2=﹣3，

∵函数的定义域为[﹣a﹣2，b]，关于原点对称，

故b=3；

（2）函数f（x）在[﹣3，3]递增，

证明如下：设x1，x2 [﹣3，3]，且x1＜x2，

则f（x1）﹣f（x2）=﹣=，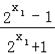

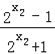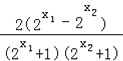∵﹣3≤x1＜x2≤3，

∴﹣＜0，

又+1＞0， +1＞0，

∴f（x1）﹣f（x2）＜0，

∴f（x1）＜f（x2），

∴f（x）在[﹣3，3]单调递增；

（3）由（1）得f（x）在[﹣3，3]递增，

又f（m﹣1）＜f（1﹣2m），

∴，

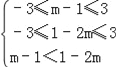解得：﹣1≤m＜，

∴实数m的取值范围[﹣1，）．