题目内容
如图,在棱长为2的正方体ABCD-EFGH中,M为DH的中点.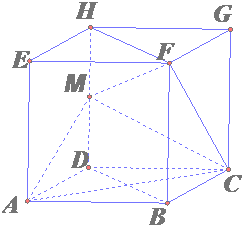
(1)求证:FC∥平面ADHE;
(2)求FM的长;
(3)求证:平面BDHF⊥平面AMC.
分析:(1)要证FC∥平面ADHE,可考虑利用线面平行的判定定理,故需要在平面ADHE内找一直线,使其与直线FC平行
,故考虑连接ED,由EF=CD,且EF∥CD,可得FC∥ED,故可证
(2)在直角三角形FMH中,利用勾股FM2=FH2+HM2,可求FM
(3)由HD⊥平面ABCD可得,AC⊥HD,又AC⊥BD可证AC⊥平面BDHF,从而可证
,故考虑连接ED,由EF=CD,且EF∥CD,可得FC∥ED,故可证
(2)在直角三角形FMH中,利用勾股FM2=FH2+HM2,可求FM
(3)由HD⊥平面ABCD可得,AC⊥HD,又AC⊥BD可证AC⊥平面BDHF,从而可证
解答:证明:(1)连接ED,因为 EF=CD,并且EF∥CD,所以FC∥ED
因为ED?平面ADHE,FC?平面ADHE,
所以FC∥平面ADHE
(2)因为HM=1,FH=2
在直角三角形FMH中,FM2=FH2+HM2,所以FM=3
(3)因为HD⊥平面ABCD,所以AC⊥HD,又因为AC⊥BD,BD∩DH=D,所以AC⊥平面BDHF
又AC?平面AMC,则平面BDHF⊥平面AMC
因为ED?平面ADHE,FC?平面ADHE,
所以FC∥平面ADHE
(2)因为HM=1,FH=2
| 2 |
在直角三角形FMH中,FM2=FH2+HM2,所以FM=3
(3)因为HD⊥平面ABCD,所以AC⊥HD,又因为AC⊥BD,BD∩DH=D,所以AC⊥平面BDHF
又AC?平面AMC,则平面BDHF⊥平面AMC
点评:本题主要考查了直线与平面平行的判定定理的应用及面面垂直的判定定理的应用,解决问题的关键是要根据题目中的条件,添加合适的辅助线,通过线线的关系、线面关系、面面关系的相互转化,达到目的.

练习册系列答案
相关题目
 如图,在棱长为2的正四面体A-BCD中,若以△ABC为视角正面,则其正视图的面积是( )
如图,在棱长为2的正四面体A-BCD中,若以△ABC为视角正面,则其正视图的面积是( )






