题目内容
已知定义在R上的函f（x）的图象关于点（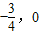
）对称，且满足f（x）=-f（x+
），f（0）=2，f（1）=-1，则f（1）+f（2）+f（3）+…+f（2009）的值是（ ）A．1
B．-1
C．2
D．-2
【答案】分析：根据题意可推出f（x）=f（x+3）且f（x）=f（-x），得到f（-1）+f（0）+f（1）=0，
故可得 f（1）+f（2）+f（3）+…+f （2009 ）=669×0+f（1）+f（2）=f（1）+f（-1）．
解答：解：定义在R上的函f（x）的图象关于点（
）对称，∴f（x）=-f（-x-
），
又f（x）=-f（x+
），∴f（x）=f（x+3）且f（x）=f（-x），
∴f（-1）=f（1）=-1，∴f（-1）+f（0）+f（1）=0．
又 2009=669×3+2，故 f（1）+f（2）+f（3）+…+f （2009 ）=669×0+f（1）+f（2）=
f（1）+f（-1）=-2，
故选 D．
点评：本题考查函数的对称性、周期性，及函数值，推出f（x）=f（x+3）且f（x）=f（-x），是解题的关键．
故可得 f（1）+f（2）+f（3）+…+f （2009 ）=669×0+f（1）+f（2）=f（1）+f（-1）．
解答：解：定义在R上的函f（x）的图象关于点（
）对称，∴f（x）=-f（-x- ），又f（x）=-f（x+
），∴f（x）=f（x+3）且f（x）=f（-x），∴f（-1）=f（1）=-1，∴f（-1）+f（0）+f（1）=0．
又 2009=669×3+2，故 f（1）+f（2）+f（3）+…+f （2009 ）=669×0+f（1）+f（2）=
f（1）+f（-1）=-2，
故选 D．
点评：本题考查函数的对称性、周期性，及函数值，推出f（x）=f（x+3）且f（x）=f（-x），是解题的关键．
练习册系列答案
相关题目
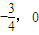）对称，且满足f（x）=-f（x+
），f（0）=2，f（1）=-1，则f（1）+f（2）+f（3）+…+f（2009）的值是（ ）