题目内容
已知:函数![]() .
.
(I)证明:f(x)与f-1(x)的交点必在在直线y=x上.
(II)是否存在一对反函数图象的交点不一定在直线y=x上,若存在,请举例说明;若不存,请说明理由.
(III)研究(I)和(II),能否得出一般性的结论,并进行证明.
解析:
|
解答:(I)y=2x+1与其反函数 (II) (III)研究(I)和(II)能得出:如果函数f(x)是增函数,并且f(x)的图象与其反函数的图象有交点,则交点一定在直线y=x上; 如果函数f(x)是减函数,并且f(x)的图象与其反函数的图象有交点,则交点不一定在直线y=x上. 证明:设点(a,b)是f(x)的图象与其反函数图象的任一交点,由于原函数与反函数图象关于直线y=x对称,则点(b,a)也是f(x)的图象与其反函数图象的交点,且有b=f(a),a=f(b) 若a=b时,交点显然在直线y=x上. 若a<b,且f(x)是增函数时,有f(b)<f(a),从而有b<a,矛盾;若b<a且f(x)是增函数时,有f(a)<f(b),从而有a<b,矛盾. 若a<b,且f(x)是减函数,有f(b)<f(a),从而a<b成立,此时交点不在直线y=x上;同理,b<a且f(x)是减函数时,交点也不在直线y=x上. 综上所述,如果函数f(x)是增函数,并且f(x)的图象与其反函数的图象有交点,则交点一定在直线y=x上; 如果函数f(x)是减函数,并且f(x)的图象与其反函数的图象有交点,则交点不一定在直线y=x上. |
提示:
|
分析:问题(I)易于解答,而问题(II)解答必须认真思考f(x)的性质,从性质的差异去寻求特例.问题(III)的证明着眼于函数单调性的差异解答. 说明:试题紧扣江苏新考纲,突显解决问题的探索性和研究性.试题难度较大. |

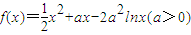
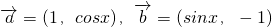 ,函数
,函数
 ,函数
,函数
 ,函数
,函数
 ,函数
,函数