题目内容
已知:函数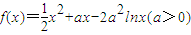
(I)求f(x)的单调区间;
(II)若f(x)>0恒成立,求a的取值范围.
【答案】分析:(I)先求出函数的定义域,进而根据函数的解析式,求出函数的导函数,分析导函数符号在不同区间上的取值,根据导函数符号与原函数的单调性之间的关系可得结论;
(II)若f(x)>0恒成立,则f(x)的最小值大于0,根据(I)中结论,求出函数的最小值,代入构造关于a的不等式,解不等式可得a的取值范围
解答:解:(I)∵函数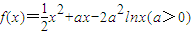 的定义域为(0,+∞)
的定义域为(0,+∞)
∴ =
=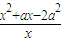 =
=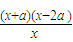
∵a>0,令f′(x)=0,则x=-a(舍去),或x=2a
∵当x∈(0,2a)时,f′(x)<0,∵当x∈(2a,+∞)时,f′(x)>0,
∴(0,2a)为函数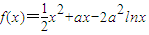 的单调递减区间,
的单调递减区间,
(2a,+∞)为函数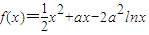 的单调递增区间;
的单调递增区间;
(II)由(I)得当x=2a时,函数取最小值4a2-2a2ln(2a)
若f(x)>0恒成立
则4a2-2a2ln(2a)=2a2•[2-ln(2a)]>0
即2-ln(2a)>0
解得a<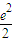
又∵a>0,
∴a的取值范围为(0,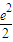 )
)
点评:本题考查的知识点是利用导数求函数的单调区间和最值,其中熟练掌握导函数符号与原函数的单调性之间的关系,是解答的关键.
(II)若f(x)>0恒成立,则f(x)的最小值大于0,根据(I)中结论,求出函数的最小值,代入构造关于a的不等式,解不等式可得a的取值范围
解答:解:(I)∵函数
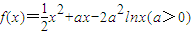 的定义域为(0,+∞)
的定义域为(0,+∞)∴
 =
=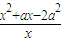 =
=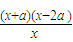
∵a>0,令f′(x)=0,则x=-a(舍去),或x=2a
∵当x∈(0,2a)时,f′(x)<0,∵当x∈(2a,+∞)时,f′(x)>0,
∴(0,2a)为函数
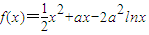 的单调递减区间,
的单调递减区间,(2a,+∞)为函数
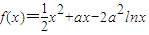 的单调递增区间;
的单调递增区间;(II)由(I)得当x=2a时,函数取最小值4a2-2a2ln(2a)
若f(x)>0恒成立
则4a2-2a2ln(2a)=2a2•[2-ln(2a)]>0
即2-ln(2a)>0
解得a<
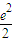
又∵a>0,
∴a的取值范围为(0,
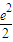 )
)点评:本题考查的知识点是利用导数求函数的单调区间和最值,其中熟练掌握导函数符号与原函数的单调性之间的关系,是解答的关键.

练习册系列答案
相关题目
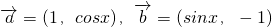 ,函数
,函数
 ,函数
,函数
 ,函数
,函数
 ,函数
,函数