题目内容
已知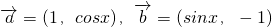 ,函数
,函数
(I)求函数f(x)的单调递增区间;
(Ⅱ)当x∈[0,π]时,求函数f(x)的最大值.
解:(I)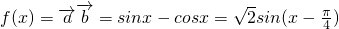 .
.
由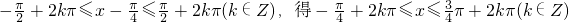 ,
,
∴f(x)的单调递增区间是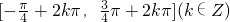 .
.
(Ⅱ)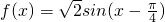 ,
,
∵x∈[0,π],∴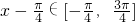 ,
,
∴当 .
.
分析:(I)利用向量的数量积公式求出f(x),据公式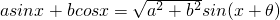 化简f(x);令整体角在正弦的递增区间上,求出x的范围为f(x)的递增区间
化简f(x);令整体角在正弦的递增区间上,求出x的范围为f(x)的递增区间
(II)先求出整体角的范围,利用三角函数的单调性求出f(x)的最大值.
点评:本题考查向量的数量积公式、考查三角函数的公式 、考查求三角函数的单调性,最值,求对称性问题时常用整体角处理的方法.
、考查求三角函数的单调性,最值,求对称性问题时常用整体角处理的方法.
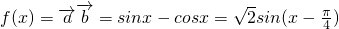 .
.由
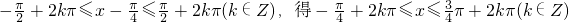 ,
,∴f(x)的单调递增区间是
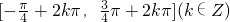 .
.(Ⅱ)
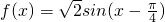 ,
,∵x∈[0,π],∴
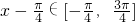 ,
,∴当
 .
.分析:(I)利用向量的数量积公式求出f(x),据公式
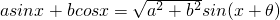 化简f(x);令整体角在正弦的递增区间上,求出x的范围为f(x)的递增区间
化简f(x);令整体角在正弦的递增区间上,求出x的范围为f(x)的递增区间(II)先求出整体角的范围,利用三角函数的单调性求出f(x)的最大值.
点评:本题考查向量的数量积公式、考查三角函数的公式
 、考查求三角函数的单调性,最值,求对称性问题时常用整体角处理的方法.
、考查求三角函数的单调性,最值,求对称性问题时常用整体角处理的方法. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的 部 分 图 象如 图 所示.
的 部 分 图 象如 图 所示. 的
解 析 式;
的
解 析 式; 中,角
中,角 的
对 边 分 别 是
的
对 边 分 别 是 ,若
,若 的
取 值 范 围.
的
取 值 范 围.