题目内容
已知函数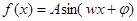 ,
,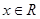 ,(其中
,(其中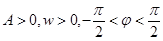 ),其部分图象如图所示。
),其部分图象如图所示。
(1)求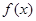 的解析式;
的解析式;
(2)求函数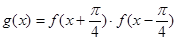 在区间
在区间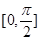 上的最大值及相应的
上的最大值及相应的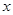 值。
值。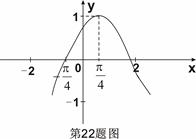
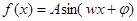 ,
,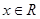 ,(其中
,(其中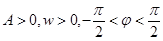 ),其部分图象如图所示。
),其部分图象如图所示。(1)求
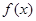 的解析式;
的解析式;(2)求函数
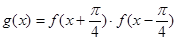 在区间
在区间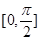 上的最大值及相应的
上的最大值及相应的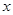 值。
值。
(I)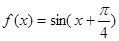 (II)当
(II)当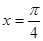 时,
时,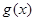 取得最大值
取得最大值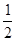 。
。
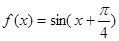 (II)当
(II)当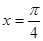 时,
时,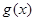 取得最大值
取得最大值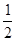 。
。正弦函数图像中最值点与相邻零点之间的横标距离是 ,从而确定
,从而确定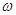 ,再必须代入最值点求得
,再必须代入最值点求得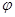 确定解析式
确定解析式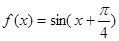 ;
;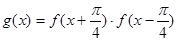 ==
==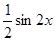 ,在区间
,在区间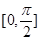 上用整体法:
上用整体法: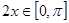 ,
,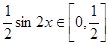
解:(I)由题图可知,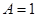
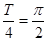 ,所以
,所以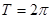 ,
, 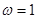 …3分
…3分
又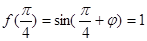 ,且
,且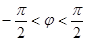 ,所以
,所以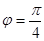 ,……………5分
,……………5分
所以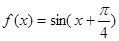 。………6分
。………6分
(II)由(I)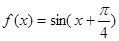 ……………10分
……………10分
所以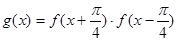 =
=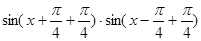 =
=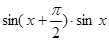 …8分
…8分
=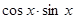 =
=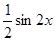 。……………10分
。……………10分
因为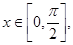 所以
所以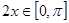 ,
,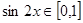 ,故
,故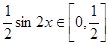 ,
,
当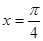 时,
时,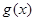 取得最大值
取得最大值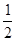
 ,从而确定
,从而确定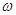 ,再必须代入最值点求得
,再必须代入最值点求得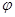 确定解析式
确定解析式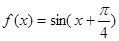 ;
;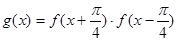 ==
==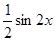 ,在区间
,在区间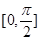 上用整体法:
上用整体法: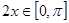 ,
,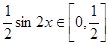
解:(I)由题图可知,
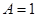
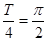 ,所以
,所以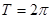 ,
, 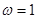 …3分
…3分又
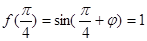 ,且
,且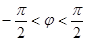 ,所以
,所以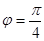 ,……………5分
,……………5分所以
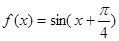 。………6分
。………6分(II)由(I)
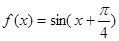 ……………10分
……………10分所以
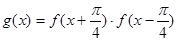 =
=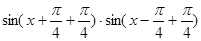 =
=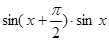 …8分
…8分=
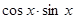 =
=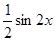 。……………10分
。……………10分因为
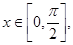 所以
所以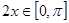 ,
,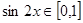 ,故
,故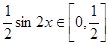 ,
,当
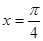 时,
时,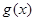 取得最大值
取得最大值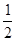

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
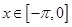 ,且
,且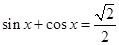 ,
,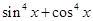 的值;
的值;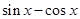 的值.
的值.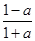 ,cosθ=
,cosθ=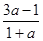 ,若θ为第二象限角,求实数a的值.
,若θ为第二象限角,求实数a的值.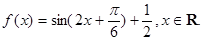
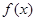 的最小正周期;
的最小正周期;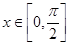 ,求函数
,求函数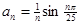 ,
,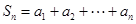 . 在
. 在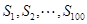 中,正数的个数是( )
中,正数的个数是( )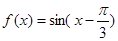 的单调递增区间为___________.
的单调递增区间为___________.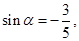
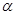 是第三象限角,则
是第三象限角,则 .
.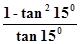 的值( )
的值( )



 ,且
,且 ,则
,则 的值为
的值为


