题目内容
 如图,已知空间四边形ABCD的对角线AC=10,BD=6,M、N分别是AB、CD的中点,MN=7,求异面直线AC与BD所成的角.
如图,已知空间四边形ABCD的对角线AC=10,BD=6,M、N分别是AB、CD的中点,MN=7,求异面直线AC与BD所成的角.
分析:先通过取中点,将两条异面直线AC与BD平移到同一个起点E,得到∠MEN或补角就是异面直线所成的角,在三角形MEN中再利用余弦定理求出此角即可.
解答: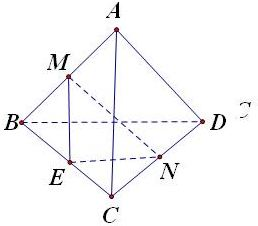 解:如图
解:如图
取BC的中点E,连接EN、EM,
∴∠MEN是异面直线AC与BD所成的角或其补角.
在△EMN中,EN=
=3,EM=
=5,MN=7,
cos∠MEN=-
,∴∠MEN=120°.
∴异面直线AC与BD所成的角是60°.
 解:如图
解:如图取BC的中点E,连接EN、EM,
∴∠MEN是异面直线AC与BD所成的角或其补角.
在△EMN中,EN=
| BD |
| 2 |
| AC |
| 2 |
cos∠MEN=-
| 1 |
| 2 |
∴异面直线AC与BD所成的角是60°.
点评:本小题主要考查异面直线所成的角,考查空间想象能力、运算能力和推理论证能力,属于基础题.

练习册系列答案
相关题目
 如图,已知空间四边形ABCD中,BC=AC,AD=BD,E是AB的中点.
如图,已知空间四边形ABCD中,BC=AC,AD=BD,E是AB的中点.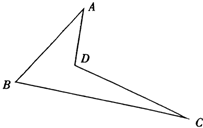 如图,已知空间四边形ABCD中,
如图,已知空间四边形ABCD中, 如图,已知空间四边形ABCD中,AB=CD=3,E、F分别是BC、AD上的点,并且BE:EC=AF:FD=1:2,EF=
如图,已知空间四边形ABCD中,AB=CD=3,E、F分别是BC、AD上的点,并且BE:EC=AF:FD=1:2,EF=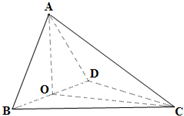 如图,已知空间四边形ABCD中,O是对角线BD的中点,
如图,已知空间四边形ABCD中,O是对角线BD的中点,