题目内容
圆C1的方程为(x-3)2+y2=
,圆C2的方程(x-3-
)2+(y-
)2=
(t∈R),过C2上任意一点作圆C1的两条切线PM、PN,切点分别为M、N,设PM与PN夹角的最大值为θ,则( )
| 4 |
| 25 |
| 1-t2 |
| 1+t2 |
| 2t |
| 1+t2 |
| 1 |
| 25 |
A、θ=
| ||
B、θ=
| ||
C、θ=
| ||
| D、θ与t的取值有关 |
分析:由圆C2的方程找出圆心所在曲线的参数方程,化为普通方程,在坐标系找出画出圆心C2所在的轨迹,找出特殊位置C2在x轴上时,圆C2与x轴右边交于A点,同时画出圆C1的图象,过A作圆C1的两条切线AM和AN,切点分别为M和N,在直角三角形AC1M中,根据直角三角形中一直角边等于斜边的一半得到这条直角边所对的角为30°,再根据切线的性质得到∠MAN的度数即为AM与AN夹角的最大值为θ的度数.
解答:解:由圆C2的方程得到圆心所在曲线的参数方程为
,
化为普通方程为(x-3)2+y2=1,又圆C1的方程为(x-3)2+y2=
,
根据题意画出图形,如图所示:
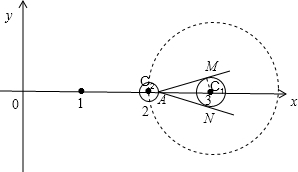
∵在Rt△AMC2中,|MC2|=
,|AC1|=1-
=
,即|AC1|=2|MC2|,
∴∠MAC1=
,即∠MAN=
,
则PM与PN夹角的最大值为θ为
.
故选B
|
化为普通方程为(x-3)2+y2=1,又圆C1的方程为(x-3)2+y2=
| 4 |
| 25 |
根据题意画出图形,如图所示:

∵在Rt△AMC2中,|MC2|=
| 2 |
| 5 |
| 1 |
| 5 |
| 4 |
| 5 |
∴∠MAC1=
| π |
| 6 |
| π |
| 3 |
则PM与PN夹角的最大值为θ为
| π |
| 3 |
故选B
点评:此题考查了圆的标准方程,圆的参数方程,两直线夹角到角的问题,直角三角形的性质,以及切线的性质,利用了数形结合的思想,其中找出圆C2上的点P在点A位置时,AM与AN夹角的最大值为θ是解本题的关键.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
 如图,已知圆C1的方程为
如图,已知圆C1的方程为
 ,椭圆C2的方程为
,椭圆C2的方程为 ,C2的离心率为
,C2的离心率为 ,如果C1与C2相交于A、B两点,且线段AB恰为圆C1的直径,试求:
,如果C1与C2相交于A、B两点,且线段AB恰为圆C1的直径,试求: ,椭圆C2的方程为
,椭圆C2的方程为 ,C2的离心率为
,C2的离心率为 ,如果C1与C2相交于A、B两点,且线段AB恰为圆C1的直径,试求:
,如果C1与C2相交于A、B两点,且线段AB恰为圆C1的直径,试求: