题目内容
如图所示,已知A,B分别为椭圆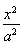 +
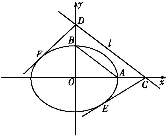
+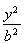 =1(a>b>0)的右顶点和上顶点,直线l∥AB,l与x轴、y轴分别交于C,D两点,直线CE,DF为椭圆的切线,则CE与DF的斜率之积kCE·kDF等于( )
=1(a>b>0)的右顶点和上顶点,直线l∥AB,l与x轴、y轴分别交于C,D两点,直线CE,DF为椭圆的切线,则CE与DF的斜率之积kCE·kDF等于( )
(A)±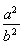 (B)±
(B)±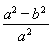
(C)±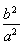 (D)±
(D)±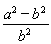
【答案】
C
【解析】由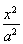 +
+ =1(a>b>0)可知A(a,0),B(0,b),
=1(a>b>0)可知A(a,0),B(0,b),
∴kAB=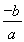 .
.
设l方程为y=-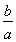 x+m,
x+m,
则C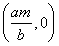 ,D(0,m).
,D(0,m).
DF方程为y=kDFx+m,
由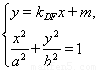
得(b2+a2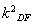 )x2+2a2mkDFx+a2m2-a2b2=0,
)x2+2a2mkDFx+a2m2-a2b2=0,
∵DF与椭圆相切,
∴Δ=(2a2mkDF)2-4(b2+a2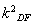 )·(a2m2-a2b2)=0,
)·(a2m2-a2b2)=0,
得 =
=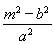 .
.
直线CE的方程为y=kCE(x-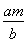 ),
),
由
得(b2+a2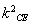 )x2-
)x2-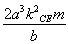 x+
x+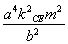 -a2b2=0.
-a2b2=0.
∵CE与椭圆相切,
∴Δ=(-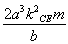 )2-4(b2+a2
)2-4(b2+a2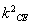 )·(
)·(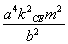 -a2b2)=0.
-a2b2)=0.
化简得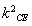 =
=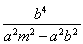 .
.
∴ ·
·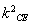 =
=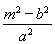 ·
·
= ,
,
∴kDF·kCE=±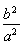 .
.

练习册系列答案
相关题目
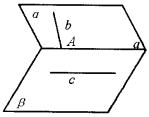
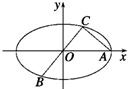 如图所示,已知A,B,C是椭圆
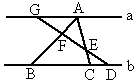
如图所示,已知A,B,C是椭圆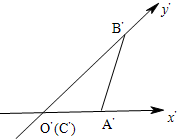 水平放置的△ABC斜二测直观图如图所示,已知A′C′=3,B′C′=2,则△ABC中AB边上中线的实际长度为
水平放置的△ABC斜二测直观图如图所示,已知A′C′=3,B′C′=2,则△ABC中AB边上中线的实际长度为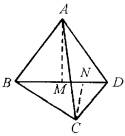

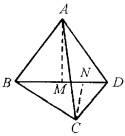
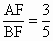 ,
,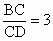 ,则AE∶EC=________.
,则AE∶EC=________.