题目内容
【题目】如图,AB为⊙O的直径,F为弦AC的中点,连接OF并延长交 ![]() 于点D,过点D作⊙O的切线,交BA的延长线于点E.
于点D,过点D作⊙O的切线,交BA的延长线于点E.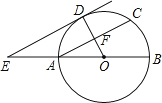
(1)求证:AC∥DE;
(2)连接CD,若OA=AE=a,写出求四边形ACDE面积的思路.
【答案】
(1)
证明:∵ED与⊙O相切于D,
∴OD⊥DE,
∵F为弦AC中点,
∴OD⊥AC,
∴AC∥DE.
(2)
解:作DM⊥OA于M,连接CD,CO,AD.
首先证明四边形ACDE是平行四边形,根据S平行四边形ACDE=AEDM,只要求出DM即可.
∵AC∥DE,AE=AO,
∴OF=DF,
∵AF⊥DO,
∴AD=AO,
∴AD=AO=OD,
∴△ADO是等边三角形,同理△CDO也是等边三角形,
∴∠CDO=∠DOA=60°,AE=CD=AD=AO=DD=a,
∴AO∥CD,又AE=CD,
∴四边形ACDE是平行四边形,易知DM= ![]() a,
a,
∴平行四边形ACDE面积= ![]() a2.
a2.

【解析】本题考查切线的性质、平行四边形的性质、垂径定理等知识,解题的关键是学会添加常用辅助线,利用特殊三角形解决问题,属于中考常考题型.(1)欲证明AC∥DE,只要证明AC⊥OD,ED⊥OD即可.(2)作DM⊥OA于M,连接CD,CO,AD,首先证明四边形ACDE是平行四边形,根据S平行四边形ACDE=AEDM,只要求出DM即可.
【考点精析】根据题目的已知条件,利用平行四边形的性质和垂径定理的推论的相关知识可以得到问题的答案,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;推论1:A、平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧B、弦的垂直平分线经过圆心,并且平分弦所对的两条弧C、平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧;推论2 :圆的两条平行弦所夹的弧相等.

 阅读快车系列答案
阅读快车系列答案【题目】某校准备组织师生共60人,从南靖乘动车前往厦门参加夏令营活动,动车票价格如表所示:(教师按成人票价购买,学生按学生票价购买).
运行区间 | 成人票价(元/张) | 学生票价(元/张) | ||
出发站 | 终点站 | 一等座 | 二等座 | 二等座 |
南靖 | 厦门 | 26 | 22 | 16 |
若师生均购买二等座票,则共需1020元.
(1)参加活动的教师有人,学生有人;
(2)由于部分教师需提早前往做准备工作,这部分教师均购买一等座票,而后续前往的教师和学生均购买二等座票.设提早前往的教师有x人,购买一、二等座票全部费用为y元.
①求y关于x的函数关系式;
②若购买一、二等座票全部费用不多于1032元,则提早前往的教师最多只能多少人?
【题目】“五一”假期期间,某餐厅对选择![]() 、
、![]() 、
、![]() 三种套餐的顾客进行优惠。对选择
三种套餐的顾客进行优惠。对选择![]() 、
、![]() 套餐的顾客都优惠10元,对选择
套餐的顾客都优惠10元,对选择![]() 套餐的顾客优惠20元。根据以往“五一”假期期间100名顾客对选择
套餐的顾客优惠20元。根据以往“五一”假期期间100名顾客对选择![]() 、
、![]() 、
、![]() 三种套餐的情况得到下表:
三种套餐的情况得到下表:
选择套餐种类 |
|
|
|
选择每种套餐的人数 | 50 | 25 | 25 |
将频率视为概率.
(I)若有甲、乙、丙三位顾客选择某种套餐,求三位顾客选择的套餐至少有两样不同的概率;
(II)若用随机变量![]() 表示两位顾客所得优惠金额的综合,求
表示两位顾客所得优惠金额的综合,求![]() 的分布列和期望。
的分布列和期望。
【题目】【2015高考福建文数】全网传播的融合指数是衡量电视媒体在中国网民中影响了的综合指标.根据相关报道提供的全网传播2015年某全国性大型活动的“省级卫视新闻台”融合指数的数据,对名列前20名的“省级卫视新闻台”的融合指数进行分组统计,结果如表所示.
组号 | 分组 | 频数 |
1 | | 2 |
2 | | 8 |
3 | | 7 |
4 | | 3 |
(Ⅰ)现从融合指数在![]() 和
和![]() 内的“省级卫视新闻台”中随机抽取2家进行调研,求至少有1家的融合指数在
内的“省级卫视新闻台”中随机抽取2家进行调研,求至少有1家的融合指数在![]() 的概率;
的概率;
(Ⅱ)根据分组统计表求这20家“省级卫视新闻台”的融合指数的平均数.