题目内容
已知函数f(x)=Asin(ωx+φ),x∈R(其中A>0,ω>0,0<φ<| π |
| 2 |
| π |
| 2 |
| 2π |
| 3 |
(1)求f(x)的解析式;
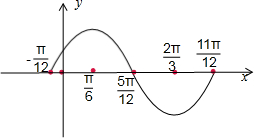
(2)用五点作图法做出f(x)的图象
(3)说明y=f(x)的图象是由y=sinx的图象经过怎样的变换得到?
(4)求函数的单调递减区间
(5)当x∈[
| π |
| 12 |
| π |
| 2 |
分析:(1)直接求出函数的周期T,A以及ω,通过函数经过的特殊点求出φ,得到函数的解析式;
(2)根据函数的解析式,通过列表,描点,连线画出函数的图象.
(3)利用图象平移的规律:左加右减,加减的单位是自变量x的变化的单位;图象伸缩变换的规律:横坐标变为坐标系x乘的数的倒数;纵坐标变为三角函数前面乘的数倍.
(4)找出正弦函数的一个递减区间,令2x+
属于这个区间列出关于x的不等式,再由x的范围求出不等式的解集,即为函数的单调递减区间.
(5)根据x的范围,求出2x+
的范围,然后求出函数值的范围.
(2)根据函数的解析式,通过列表,描点,连线画出函数的图象.
(3)利用图象平移的规律:左加右减,加减的单位是自变量x的变化的单位;图象伸缩变换的规律:横坐标变为坐标系x乘的数的倒数;纵坐标变为三角函数前面乘的数倍.
(4)找出正弦函数的一个递减区间,令2x+
| π |
| 6 |
(5)根据x的范围,求出2x+
| π |
| 6 |
解答:解:(1)由题意可知,T=
×2=π,A=2,ω=
=2,
∵2sin(2•
+φ) =-2,∴φ=
+2kπ,k∈Z,∵0<φ<
∴φ=
所以函数:f(x)=2sin(2x+
).
(2)f(x)=2sin(2x+
).
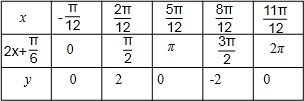
列表
(3)将由y=sinx的图象向左平移
,得到函数y=sin(x+
)
再横坐标缩小到原来的
倍,纵坐标不变得到函数y=sin(2x+
)
再横坐标不变,纵坐标变为原来的倍得到y=2sin(2x+
).
(4)∵正弦函数的单调递减区间为[2kπ-
,2kπ-
],
∴2kπ-
≤2x+
≤-
+2kπ,
解得kπ-
≤x≤kπ-
,k∈Z;
(5)当x∈[
,
],2x+
∈[
,
],2sin(2x+
)∈[-1,2],所以f(x)的值域为:[-1,2].
| π |
| 2 |
| 2π |
| T |
∵2sin(2•
| 2π |
| 3 |
| π |
| 6 |
| π |
| 2 |
∴φ=
| π |
| 6 |
所以函数:f(x)=2sin(2x+
| π |
| 6 |
(2)f(x)=2sin(2x+
| π |
| 6 |
列表


(3)将由y=sinx的图象向左平移
| π |
| 6 |
| π |
| 6 |
再横坐标缩小到原来的
| 1 |
| 2 |
| π |
| 6 |
再横坐标不变,纵坐标变为原来的倍得到y=2sin(2x+
| π |
| 6 |
(4)∵正弦函数的单调递减区间为[2kπ-
| 3π |
| 2 |
| π |
| 2 |
∴2kπ-
| 3π |
| 2 |
| π |
| 6 |
| π |
| 2 |
解得kπ-
| 5π |
| 6 |
| π |
| 3 |
(5)当x∈[
| π |
| 12 |
| π |
| 2 |
| π |
| 6 |
| π |
| 3 |
| 7π |
| 6 |
| π |
| 6 |
点评:本题是中档题,考查三角函数的解析式的求法,五点法作图,函数的单调性的应用,函数图象的平移伸缩变换,函数的最值,可以说一题概括三角函数的基本知识的灵活应用,考查计算能力.

练习册系列答案
相关题目