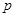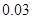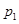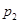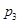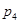题目内容
(本小题满分12分)在某学校组织的一次篮球定点投篮训练中,规定每人最多投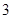 次:在
次:在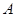 处每投进一球得
处每投进一球得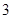 分,在
分,在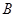 处每投进一球得
处每投进一球得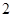 分;如果前两次得分之和超过
分;如果前两次得分之和超过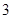 分即停止投篮,否则投第三次.某同学在
分即停止投篮,否则投第三次.某同学在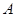 处的命中率
处的命中率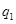 为
为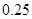 ,在
,在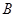 处的命中率为
处的命中率为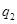 ,该同学选择先在
,该同学选择先在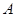 处投一球,以后都在
处投一球,以后都在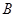 处投,用
处投,用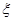 表示该同学投篮训练结束后所得的总分,其分布列为
表示该同学投篮训练结束后所得的总分,其分布列为
|
|
0 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
|
(1) 求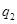 的值;
的值; (2)
求随机变量
(2)
求随机变量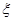 的数学期望
的数学期望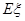 ;
;
(3) 试比较该同学选择都在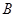 处投篮得分超过
处投篮得分超过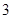 分与选择上述方式投篮得分超过
分与选择上述方式投篮得分超过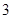 分的概率的大小.
分的概率的大小.
【答案】
(1)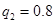 ;
;
(2)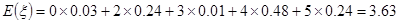 ;
;
(3)该同学选择都在B处得分超过3分的概率大于该同学选择第一次在A处以后都在B处投得分超过3分的概率。
【解析】本题考查随机变量的分布列与数学期望,明确变量的含义,求出概率是解题的关键.
(1)设该同学在A处投中为事件A,在B处投中为事件B,则事件A,B相互独立,ξ=0时,对应事件
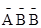 ,根据分布列,即可求得q2的值;
,根据分布列,即可求得q2的值;
(2)明确ξ=2、3、4、5,对应的事件,求出相应的概率,即可得到随机变量ξ的分布列与数学期望Eξ.
(3)因为设“同学选择A处投,以后再B处投得分超过3分”为事件A
设“同学选择都在B处投得分超过3分”为事件B
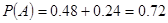
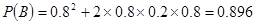
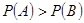
(1)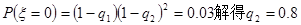 (3’)
(3’)
(2)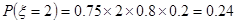
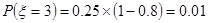
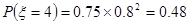
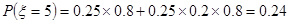
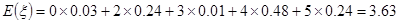 (9’)
(9’)
(3)设“同学选择A处投,以后再B处投得分超过3分”为事件A
设“同学选择都在B处投得分超过3分”为事件B
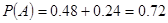
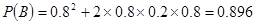
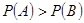 ,该同学选择都在B处得分超过3分的概率大于该同学选择第一次在A处以后都在B处投得分超过3分的概率。 (12’)
,该同学选择都在B处得分超过3分的概率大于该同学选择第一次在A处以后都在B处投得分超过3分的概率。 (12’)

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目