题目内容
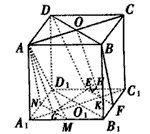
在棱长为α的正方体ABCD- A1B1C1D1中,设M、N、E、F分别是棱A1B1、A1D1、C1D1、B1C1的中点.
(1)求证:E、F、B、D四点共面;
(2)求证:平面AMN∥平面EFDB;
(3)求平面AMN和平面BFED间的距离.
(1)求证:E、F、B、D四点共面;
(2)求证:平面AMN∥平面EFDB;
(3)求平面AMN和平面BFED间的距离.
(1)证明: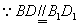 ,而E、F分别是 ,而E、F分别是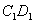 、 、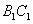 的中点, 的中点,∴ 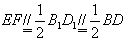 , ,∴E、F、B、D四点共面. |
|
| (2)证明:连结AC交BD于O点,连结A′C′,交MN、EF于G、K, 连结AG、OK, 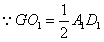 , ,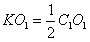 , ,∴ 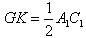 , ,又 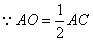 且 且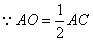 , ,∴ 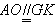 ,∴四边形AOKG为平行四边形 ,∴AG∥OK, ,∴四边形AOKG为平行四边形 ,∴AG∥OK,∴AG∥平面BEFD, 又 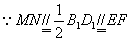 , ,∴MN∥平面BFED, ∴平面AMN∥平面BFED. (3)解:过G作GH⊥OK于H,则GH即为所求, 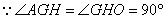 , , ∴ 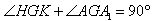 , ,又 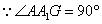 , ,∴ 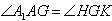 , ,又 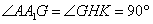 , ,∴ 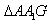 ∽△GHK,∴ ∽△GHK,∴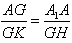 , ,又∵ 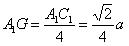 ,∴ ,∴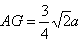 , ,又 ∵ 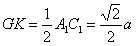 , ,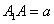 , ,∴  , ,所以,平面AMN与平面BFED之间距离为 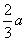 。 。 |
 |

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
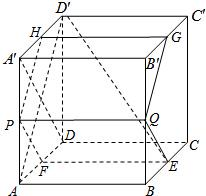 如图,在棱长为1的正方体ABCD-A′B′C′D′中,AP=BQ=b(0<b<1),截面PQEF∥A′D,截面PQGH∥AD′.
如图,在棱长为1的正方体ABCD-A′B′C′D′中,AP=BQ=b(0<b<1),截面PQEF∥A′D,截面PQGH∥AD′. (理科)如图,在棱长为1的正方体A'C中,过BD及B'C'的中点E作截面BEFD交C'D'于F.
(理科)如图,在棱长为1的正方体A'C中,过BD及B'C'的中点E作截面BEFD交C'D'于F.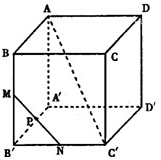 (2004•武汉模拟)(理科)在棱长为1的正方体ABCD-A′B′C′D′中,AC′为对角线,M、N分别为BB′,B′C′中点,P为线段MN中点.
(2004•武汉模拟)(理科)在棱长为1的正方体ABCD-A′B′C′D′中,AC′为对角线,M、N分别为BB′,B′C′中点,P为线段MN中点.