题目内容
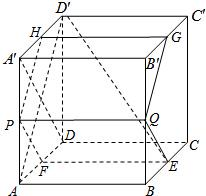 如图,在棱长为1的正方体ABCD-A′B′C′D′中,AP=BQ=b(0<b<1),截面PQEF∥A′D,截面PQGH∥AD′.
如图,在棱长为1的正方体ABCD-A′B′C′D′中,AP=BQ=b(0<b<1),截面PQEF∥A′D,截面PQGH∥AD′.(1)证明:平面PQEF和平面PQGH互相垂直;
(2)证明:截面PQEF和截面PQGH面积之和是定值,并求出这个值;
(3)若D′E与平面PQEF所成的角为45°,求D′E与平面PQGH所成角的正弦值.
分析:(解法一)
(Ⅰ)由题意得 A′D∥PF,PH∥AD′,PQ∥AB,又因AD′⊥A′D,AD′⊥AB,得到PH⊥PF,PH⊥PQ,
可证PH⊥平面PQEF,用面面垂直的判定定理即证.
(Ⅱ)由(Ⅰ)知截面PQEF和截面PQGH都是矩形,且PF=
AP,PH=
PA′,PQ=1,代入
面积公式求解.
(Ⅲ)连接BC′交EQ于点M,得到平面ABC′D′∥平面PQGH,所求的角转化到D′E与平面ABC′D′所成
角,由(Ⅰ)知EM⊥平面ABC′D则′EM与D′E的比值就是所求的正弦值,根据已知条件求出b的
值,在直角三角形中求解.
(解法二)
(Ⅰ)用数量积为零求平面PQEF的法向量
和平面PQGH的法向量
,求它们的数量积为零证出
面面垂直.
(Ⅱ)用数量积为零证出截面PQEF和截面PQGH都是矩形,用两点间的距离公式求出邻边得长度,再
求面积和.
(Ⅲ)由(Ⅰ)知平面PQEF和平面PQGH的法向量,用数量积根据已知条件先求出b的值,再求向量所
成角的余弦值.
(Ⅰ)由题意得 A′D∥PF,PH∥AD′,PQ∥AB,又因AD′⊥A′D,AD′⊥AB,得到PH⊥PF,PH⊥PQ,
可证PH⊥平面PQEF,用面面垂直的判定定理即证.
(Ⅱ)由(Ⅰ)知截面PQEF和截面PQGH都是矩形,且PF=
| 2 |
| 2 |
面积公式求解.
(Ⅲ)连接BC′交EQ于点M,得到平面ABC′D′∥平面PQGH,所求的角转化到D′E与平面ABC′D′所成
角,由(Ⅰ)知EM⊥平面ABC′D则′EM与D′E的比值就是所求的正弦值,根据已知条件求出b的
值,在直角三角形中求解.
(解法二)
(Ⅰ)用数量积为零求平面PQEF的法向量
| AD′ |
| A′D |
面面垂直.
(Ⅱ)用数量积为零证出截面PQEF和截面PQGH都是矩形,用两点间的距离公式求出邻边得长度,再
求面积和.
(Ⅲ)由(Ⅰ)知平面PQEF和平面PQGH的法向量,用数量积根据已知条件先求出b的值,再求向量所
成角的余弦值.
解答:解:解法一:
(Ⅰ)证明:∵面PQEF∥A′D,平面PQEF∩平面A′ADD′=PF
∴A′D∥PF,同理可得PH∥AD′,
∵AP=BQ=b,AP∥BQ;∴APBQ是平行四边形,∴PQ∥AB,
∵在正方体中,AD′⊥A′D,AD′⊥AB,
∴PH⊥PF,PH⊥PQ,
∴PH⊥平面PQEF,PH?平面PQGH.
∴平面PQEF⊥平面PQGH.(4分)
(Ⅱ)证明:由(Ⅰ)知
PF=
AP,PH=
PA′,截面PQEF和截面PQGH都是矩形,且PQ=1,
∴截面PQEF和截面PQGH面积之和是(
AP+
PA′)×PQ=
,是定值.(8分)
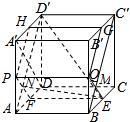 (Ⅲ)解:连接BC′交EQ于点M.
(Ⅲ)解:连接BC′交EQ于点M.
∵PH∥AD′,PQ∥AB;PH∩PQ=P,AD′∩AB=A
∴平面ABC′D′∥平面PQGH,
∴D′E与平面PQGH所成角与D′E与平面ABC′D′所成角相等.
由(Ⅰ)同理可证EQ⊥平面PQGH,可知EM⊥平面ABC′D′,
∴EM与D′E的比值就是所求的正弦值.
设AD′交PF于点N,连接EN,由FD=1-b知
D′E=
,ND′=
+
(1-b).
∵AD′⊥平面PQEF,又已知D′E与平面PQEF成45°角,
∴D′E=
ND′,即
[
+
(1-b)]=
,
解得b=
,可知E为BC中点.
∴EM=
,又D′E=
=
,
∴D′E与平面PQCH所成角的正弦值为
=
.(12分)
解法二:
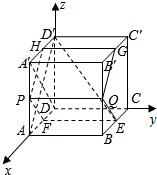
以D为原点,射线DA,DC,DD′分别为x,y,z轴的正半轴建立如图的空间直角坐标系D-xyz由已知得DF=1-b,
故A(1,0,0),A′(1,0,1),D(0,0,0),D′(0,0,1),P(1,0,b),Q(1,1,b),
E(1-b,1,0),F(1-b,0,0),G(b,1,1),H(b,0,1).
(Ⅰ)证明:在所建立的坐标系中,
可得
=(0,1,0),
=(-b,0,-b),
=(b-1,0,1-b),
=(-1,0,1),
=(-1,0,-1).
 ∵
∵
•
=0,
•
=0,∴
是平面PQEF的法向量.
∵
•
=0,
•
=0,∴
是平面PQGH的法向量.
∵
•
=0,∴
⊥
,
∴平面PQEF⊥平面PQGH.(4分)
(Ⅱ)证明:∵
=(0,-1,0),
∴
∥
,
=
,
又∵
⊥
,∴PQEF为矩形,同理PQGH为矩形.
在坐标系中可求得
=
(1-b),
=
b,
∴
+
=
,又
=1,
∴截面PQEF和截面PQGH面积之和为
,是定值.(8分)
(Ⅲ)解:由已知得
与
成45°角,又
=(1-b,1,-1),
=(-1,0,1)
可得|
|=|
|=
,
即
=1,解得b=
.
∴
=(
,1,-1),又
=(-1,0,-1),
∴D′E与平面PQGH所成角的正弦值为|cos<
,
>|=|
|=
.(12分)
(Ⅰ)证明:∵面PQEF∥A′D,平面PQEF∩平面A′ADD′=PF
∴A′D∥PF,同理可得PH∥AD′,
∵AP=BQ=b,AP∥BQ;∴APBQ是平行四边形,∴PQ∥AB,
∵在正方体中,AD′⊥A′D,AD′⊥AB,
∴PH⊥PF,PH⊥PQ,
∴PH⊥平面PQEF,PH?平面PQGH.
∴平面PQEF⊥平面PQGH.(4分)
(Ⅱ)证明:由(Ⅰ)知
PF=
| 2 |
| 2 |
∴截面PQEF和截面PQGH面积之和是(
| 2 |
| 2 |
| 2 |
 (Ⅲ)解:连接BC′交EQ于点M.
(Ⅲ)解:连接BC′交EQ于点M.∵PH∥AD′,PQ∥AB;PH∩PQ=P,AD′∩AB=A
∴平面ABC′D′∥平面PQGH,
∴D′E与平面PQGH所成角与D′E与平面ABC′D′所成角相等.
由(Ⅰ)同理可证EQ⊥平面PQGH,可知EM⊥平面ABC′D′,
∴EM与D′E的比值就是所求的正弦值.
设AD′交PF于点N,连接EN,由FD=1-b知
D′E=
| (1-b)2+2 |
| ||
| 2 |
| ||
| 2 |
∵AD′⊥平面PQEF,又已知D′E与平面PQEF成45°角,
∴D′E=
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| (1-b)2+2 |
解得b=
| 1 |
| 2 |
∴EM=
| ||
| 4 |
| (1-b)2+2 |
| 3 |
| 2 |
∴D′E与平面PQCH所成角的正弦值为
| EM |
| D′E |
| ||
| 6 |
解法二:
以D为原点,射线DA,DC,DD′分别为x,y,z轴的正半轴建立如图的空间直角坐标系D-xyz由已知得DF=1-b,
故A(1,0,0),A′(1,0,1),D(0,0,0),D′(0,0,1),P(1,0,b),Q(1,1,b),
E(1-b,1,0),F(1-b,0,0),G(b,1,1),H(b,0,1).
(Ⅰ)证明:在所建立的坐标系中,
可得
| PQ |
| PF |
| PH |
| AD′ |
| A′D |
 ∵
∵| AD′ |
| PQ |
| AD′ |
| PF |
| AD′ |
∵
| A′D |
| PQ |
| A′D |
| PH |
| A′D |
∵
| AD′ |
| A′D |
| A′D |
| AD′ |
∴平面PQEF⊥平面PQGH.(4分)
(Ⅱ)证明:∵
| EF |
∴
| EF |
| PQ |
| |EF| |
| |PQ| |
又∵
| PF |
| PQ |
在坐标系中可求得
| |PH| |
| 2 |
| |PF| |
| 2 |
∴
| |PH| |
| |PF| |
| 2 |
| |PQ| |
∴截面PQEF和截面PQGH面积之和为
| 2 |
(Ⅲ)解:由已知得
| D′E |
| AD′ |
| D′E |
| AD′ |
可得|
| ||||
|
| b-2 | ||||
|
| ||
| 2 |
即
| 2-b | ||
|
| 1 |
| 2 |
∴
| D′E |
| 1 |
| 2 |
| A′D |
∴D′E与平面PQGH所成角的正弦值为|cos<
| D′E |
| A′D |
-
| ||||
|
| ||
| 6 |
点评:本题主要考查空间中的线面、面面垂直和平行的定理,线面角的求法,解三角形等基础知识;本题为一题多解的情况,一种是向量法,另一种是几何法,对于求线面角向量法简单,因用此法;还考查转化思想与逻辑思维能力,属于难度很大的题.

练习册系列答案
相关题目
 如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
 如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
