题目内容
已知向量| e |
| OP |
| OP |
| e |
(1)求动点P的轨迹;
(2)设B、C是点P的轨迹上不同两点,满足
| OB |
| OC |
| AB |
| AC |
分析:(1)令P(x,y),由模的坐标表示与内积的坐标表示即可得到点P的轨迹方程.
(2)设BC:x=ky设B(x1,y1),C(x2,y2),将直线的方程与点P的轨迹方程联立得到B,C两点的坐标与参数k的关系,再由
⊥
,得到(x1-m)(x2-m)+y1y2=0,建立起参数m,k的方程,由其形式作出判断求参数的取值范围,若能求出则说明存在,否则说明不存在.
(2)设BC:x=ky设B(x1,y1),C(x2,y2),将直线的方程与点P的轨迹方程联立得到B,C两点的坐标与参数k的关系,再由
| AB |
| AC |
解答:解:(1)令P(x,y),则
-(x-y)•(1,0)=2
∴
=x+2即y2=4(x+1)(4分)
(2)存在?-2≤m<-1或m≥2使得
⊥
,
设BC:x=ky设B(x1,y1),C(x2,y2)
?y2-4ky-4=0
y1+y2=4k,y1y2=-4(6分)
∵
⊥
∴
•
=0
即(x1-m)(x2-m)+y1y2=0即
(k2+1)y1y2-mk(y1+y2)+m2=0(8分)
∴-4(k2+1)-mk-4k+m2=0
(4m+4)k2=m2-4(10分)
若存在则
?-2≤m<-1或m≥2.(12分)
| x2+y2 |
∴
| x2+y2 |
(2)存在?-2≤m<-1或m≥2使得
| AB |
| AC |
设BC:x=ky设B(x1,y1),C(x2,y2)
|
y1+y2=4k,y1y2=-4(6分)
∵
| AB |
| AC |
| AB |
| AC |
即(x1-m)(x2-m)+y1y2=0即
(k2+1)y1y2-mk(y1+y2)+m2=0(8分)
∴-4(k2+1)-mk-4k+m2=0
(4m+4)k2=m2-4(10分)
若存在则
|
点评:本题考查平面向量的正交分解与坐标表示,解题的关键是由向量的坐标表示与模与内积的坐标表示求出点P的轨迹方程以及利用直线与圆锥曲线的位置关系及向量的内积为0建立起参数的方程.本题综合性强运算量大,思维含量较大,极易因变形及运算出错,解题时要严谨认真.

练习册系列答案
相关题目
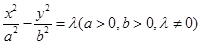 同一条渐近线上的两个不同的点,已知向量
同一条渐近线上的两个不同的点,已知向量 =(1,0),
=(1,0),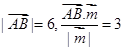 ,则双曲线的离心率e等于
,则双曲线的离心率e等于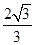 C.2或
C.2或 D. 2或
D. 2或