题目内容
已知平面α的斜线a与α内一直线b相交成θ角，且a与α相交成?1角，a在α上的射影c与b相交成?2角，则有（ ）
分析：如图．先过直线a上的一点A作AB⊥α，AC⊥c，根据线面垂直的判定定理可得，OC⊥BC，再根据三角函数可得cos∠AOB•cos∠BOC=cos∠AOC，结合选项即可得出答案．
解答：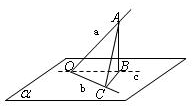
解：过直线a上的一点A作AB⊥α，AC⊥c，垂直分别为B，C．连接BC．如图．
∵AB⊥α，根据线面垂直的判定定理可得，OC⊥BC，
在Rt△OAB，cos∠AOB=cos?1=
=
，
Rt△AOC中，cos∠AOC=
=
Rt△OCB中，cos∠BOC=
∴cos∠AOB•cos∠BOC=
•
=
=cos∠AOC
∴cosθ=cos?1cos?2
故选A．
解：过直线a上的一点A作AB⊥α，AC⊥c，垂直分别为B，C．连接BC．如图．∵AB⊥α，根据线面垂直的判定定理可得，OC⊥BC，
在Rt△OAB，cos∠AOB=cos?1=
| OB |
| OA |
| ||
| 2 |
Rt△AOC中，cos∠AOC=
| OC |
| OA |
| 1 |
| 2 |
Rt△OCB中，cos∠BOC=
| OC |
| OB |
∴cos∠AOB•cos∠BOC=
| OB |
| OA |
| OC |
| OB |
| OC |
| OA |
∴cosθ=cos?1cos?2
故选A．
点评：主要考查了异面直线及其所成的角、三余弦定理的应用，解决本题的关键是要熟练应用线面垂直的判定定理找出已知角之间的余弦关系．
练习册系列答案
相关题目