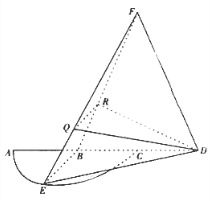
题目内容
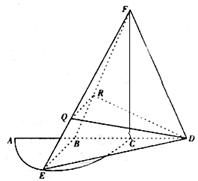
如图,
是半径为a的半圆,AC为直径,点E为
的中点,点B和点C为线段AD的三等分点,平面AEC外一点F满足FB=FD=
a,EF=
a.
(1)证明:EB⊥FD;
(2)已知点Q,R为线段FE,FB上的点,FQ=
FE,FR=
FB,求平面BED与平面RQD所成二面角的正弦值.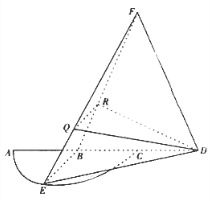
 |
| AEC |
 |
| AC |
| 5 |
| 6 |
(1)证明:EB⊥FD;
(2)已知点Q,R为线段FE,FB上的点,FQ=
| 2 |
| 3 |
| 2 |
| 3 |

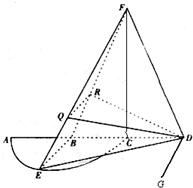
(1)证明:连接CF,因为
 |
| AEC |
 |
| AC |
在RT△BCE中,EC=
| BC2+BE2 |
| a2+a2 |
| 2 |
在△BDF中,BF=DF=
| 5 |
在△CEF中,CE2+CF2=(
| 2 |
因为CF⊥BD,CF⊥EC,且CE∩BD=C,所以CF⊥平面BED,
而EB?平面BED,∴CF⊥EB.
因为EB⊥AC,EB⊥CF,且AC∩CF=C,所以EB⊥平面BDF,
而FD?平面BDF,∴EB⊥FD.
(2)设平面BED与平面RQD的交线为DG.
由FQ=
| 2 |
| 3 |
| 2 |
| 3 |
而EB?平面BDE,∴QR∥平面BDE,
而平面BDE∩平面RQD=DG,
∴QR∥DG∥EB.
由(1)知,BE⊥平面BDF,∴DG⊥平面BDF,
而DR,DB?平面BDF,∴DG⊥DR,DG⊥DB,
∴∠RDB是平面BED与平面RQD所成二面角的平面角.
在Rt△BCF中,CF=
| BF2-BC2 |
(
|
| FC |
| BF |
| 2a | ||
|
| 2 | ||
|
| 1-sin2∠RBD |
| 1 | ||
|
在△BDR中,由FR=
| 2 |
| 3 |
| 1 |
| 3 |
| ||
| 3 |
由余弦定理得,RD=
| BD2+BR2-2BD•BRcos∠RBD |
(2a)2+(
|
| ||
| 3 |
由正弦定理得,
| BR |
| sin∠RDB |
| RD |
| sin∠RBD |
| ||||
| sin∠RDB |
| ||||
|
2
| ||
| 29 |
故平面BED与平面RQD所成二面角的正弦值为
2
| ||
| 29 |

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 如图,
如图,
 如图,弧AEC是半径为a的半圆,AC为直径,点E为弧AC的中点,点B和点C为线段AD的三等分点,平面AEC外一点F满足FC⊥平面BED,FB=
如图,弧AEC是半径为a的半圆,AC为直径,点E为弧AC的中点,点B和点C为线段AD的三等分点,平面AEC外一点F满足FC⊥平面BED,FB= 是半径为a的半圆,AC为直径,点E为弧
是半径为a的半圆,AC为直径,点E为弧 的中点,点B和点C为线段AD的三等分点.平面AEC外一点F满足FB=DF=
的中点,点B和点C为线段AD的三等分点.平面AEC外一点F满足FB=DF=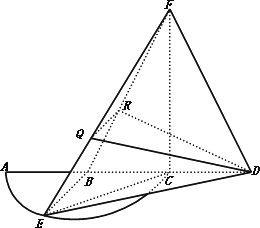
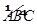 是半径为a的半圆,AC为直径,点E为
是半径为a的半圆,AC为直径,点E为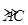 的中点,点B和点C为线段AD的三等分点.平面AEC外一点F满足
的中点,点B和点C为线段AD的三等分点.平面AEC外一点F满足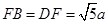 ,FE=
,FE=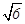 a
.
a
.
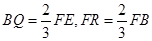 ,求平面
,求平面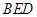 与平面
与平面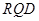 所成二面角的正弦值
所成二面角的正弦值