题目内容
过曲线y=x2上一点Q0(1,1)作曲线的切线,交x轴于点P1;过P1作垂直于x轴的直线交曲线于Q1,过Q1作曲线的切线交x轴于P2;过P2作垂直于x轴的直线交曲线于Q2;如此继续下去得到点列:P1,P2,P3,…,Pn,…,设Pn的横坐标为xn.
(Ⅰ)求x1;
(Ⅱ)求xn(用只含有字母n的代数式表示).
(Ⅲ)令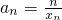 ,求数列{an}的前n项的和Sn.
,求数列{an}的前n项的和Sn.
解:(Ⅰ)因为y'=2x,所以曲线在点Q0处的切线方程为y-1=2(x-1).
令y=0,得 ,即
,即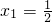 .
.
(Ⅱ)曲线在点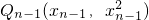 处的切线方程为
处的切线方程为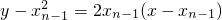 .
.
令y=0,得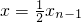 ,即
,即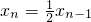 .
.
所以{xn}是以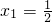 为首项,
为首项, 为公比的等比数列.
为公比的等比数列.
所以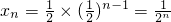 .
.
(Ⅲ)由(Ⅱ)得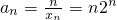 .
.
∴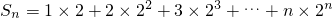 ①
①
∴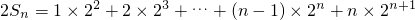 ②
②
由①-②得,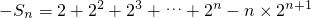 =
=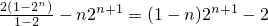 .
.
∴ .
.
分析:(Ⅰ)求导函数,求得曲线在点Q0处的切线方程,令y=0,可求x1;
(Ⅱ)曲线在点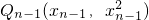 处的切线方程为
处的切线方程为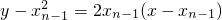 ,令y=0,得
,令y=0,得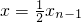 ,即
,即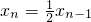 ,从而可得{xn}是以
,从而可得{xn}是以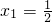 为首项,
为首项, 为公比的等比数列,由此可求xn;
为公比的等比数列,由此可求xn;
(Ⅲ)由(Ⅱ)得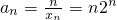 ,所以
,所以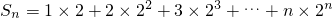 ,利用错位相减法可求数列{an}的前n项的和Sn.
,利用错位相减法可求数列{an}的前n项的和Sn.
点评:本题考查导数的几何意义,考查等比数列的判定,考查等比数列的通项,考查错位相减法求数列的和,属于中档题.
令y=0,得
 ,即
,即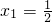 .
.(Ⅱ)曲线在点
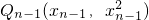 处的切线方程为
处的切线方程为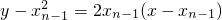 .
.令y=0,得
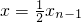 ,即
,即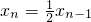 .
.所以{xn}是以
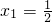 为首项,
为首项, 为公比的等比数列.
为公比的等比数列.所以
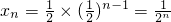 .
.(Ⅲ)由(Ⅱ)得
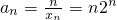 .
.∴
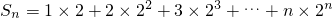 ①
①∴
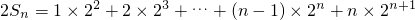 ②
②由①-②得,
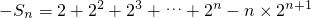 =
=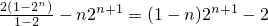 .
.∴
 .
.分析:(Ⅰ)求导函数,求得曲线在点Q0处的切线方程,令y=0,可求x1;
(Ⅱ)曲线在点
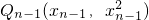 处的切线方程为
处的切线方程为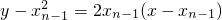 ,令y=0,得
,令y=0,得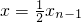 ,即
,即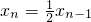 ,从而可得{xn}是以
,从而可得{xn}是以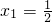 为首项,
为首项, 为公比的等比数列,由此可求xn;
为公比的等比数列,由此可求xn;(Ⅲ)由(Ⅱ)得
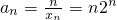 ,所以
,所以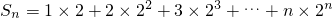 ,利用错位相减法可求数列{an}的前n项的和Sn.
,利用错位相减法可求数列{an}的前n项的和Sn.点评:本题考查导数的几何意义,考查等比数列的判定,考查等比数列的通项,考查错位相减法求数列的和,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
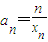 ,求数列{an}的前n项的和Sn.
,求数列{an}的前n项的和Sn.