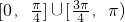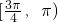题目内容
过曲线y=x2-2x+3上一点P作曲线的切线,若切点P的横坐标的取值范围是[
,
],则切线的倾斜角的取值范围是( )
| 1 |
| 2 |
| 3 |
| 2 |
分析:由导函数的几何意义可知函数图象在切点处的切线的斜率值即为其点的导函数值,结合函数的值域的求法求出k的范围,再根据k=tanα,结合正切函数的性质求出角α的范围.
解答:解:根据题意得f′(x)=2x-2,∵x∈[
,
]
∵-1≤2x-2≤1,
则曲线y=x2-2x+3上切点处的切线的斜率k:-1≤k≤1,
又∵k=tanα,结合正切函数的性质可得:
α∈[0,
]∪[
,π),
故选B.
| 1 |
| 2 |
| 3 |
| 2 |
∵-1≤2x-2≤1,
则曲线y=x2-2x+3上切点处的切线的斜率k:-1≤k≤1,
又∵k=tanα,结合正切函数的性质可得:
α∈[0,
| π |
| 4 |
| 3π |
| 4 |
故选B.
点评:本题考查了导数的几何意义、二次函数的导数、函数的值域等基本知识,以及利用正切函数的图象求倾斜角,考查运算求解能力,考查数形结合思想.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
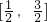 ,则切线的倾斜角的取值范围是
,则切线的倾斜角的取值范围是