题目内容
已知定义在R上的函数 满足条件
满足条件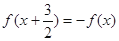 ,且函数
,且函数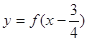 为奇函数,给出以下四个命题①函数
为奇函数,给出以下四个命题①函数 的最小正周期是
的最小正周期是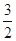 ;②函数
;②函数 的图象关于点
的图象关于点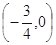 对称;③函数
对称;③函数 为R上的偶函数;④函数
为R上的偶函数;④函数 为R上的单调函数。其中真命题的个数是( )
为R上的单调函数。其中真命题的个数是( )
| A.1 | B.2 | C.3 | D.4 |
B
解析试题分析:由①可得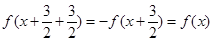 所以最小正周期为3,故①错;因为
所以最小正周期为3,故①错;因为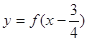 是奇函数,相当于是把f(x)向右平移
是奇函数,相当于是把f(x)向右平移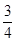 个单位后图象关于原点对称,则f(x)关于
个单位后图象关于原点对称,则f(x)关于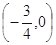 故②正确;对于③:由②知,对于任意的x∈R,都有
故②正确;对于③:由②知,对于任意的x∈R,都有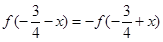 用
用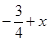 换
换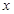 可得
可得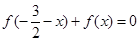 故f(x)是偶函数;由前面可知f(x)是周期函数,所以在R上不是单调函数故④错误.
故f(x)是偶函数;由前面可知f(x)是周期函数,所以在R上不是单调函数故④错误.
考点:函数的奇偶性,周期函数性质.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
函数f(x)=lnx–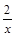 的零点所在的大致区间是( )
的零点所在的大致区间是( )
| A.(1, 2) | B.(2, 3) | C.(1, )和(3, 4) )和(3, 4) | D.(e, +∞) |
若函数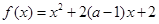 在区间
在区间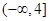 内递减,那么实数
内递减,那么实数 的取值范围为( )
的取值范围为( )
A.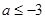 | B.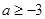 | C.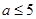 | D.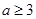 |
已知函数 ,
,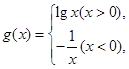 则函数
则函数 在区间
在区间 内的零点个数为( )
内的零点个数为( )
A.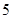 | B.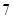 | C.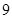 | D.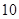 |
设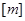 表示不超过实数
表示不超过实数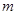 的最大整数,则在直角坐标平面
的最大整数,则在直角坐标平面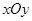 上满足
上满足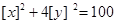 的点
的点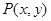 所形成的图形的面积为( )
所形成的图形的面积为( )
| A.10 | B.12 | C.10 | D.12 |
函数f(x)=xe-x,x∈[0,4]的最大值是( )
| A.0 | B. | C.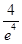 | D.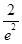 |
设函数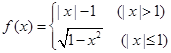 关于
关于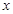 的方程
的方程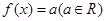 的解的个数不可能是( )
的解的个数不可能是( )
| A.1 | B.2 | C.3 | D.4 |
若函数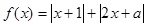 的最小值为3,则实数
的最小值为3,则实数 的值为( )
的值为( )
| A.5或8 | B.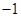 或5 或5 | C.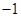 或 或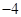 | D.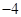 或8 或8 |
 点沿三角形列的底边匀速向前滚动(如图),设滚动中的圆与系列正三角形的重叠部分(如图中的阴影)的面积
点沿三角形列的底边匀速向前滚动(如图),设滚动中的圆与系列正三角形的重叠部分(如图中的阴影)的面积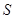 关于时间
关于时间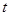 的函数为
的函数为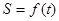 ,则下列图中与函数
,则下列图中与函数