题目内容
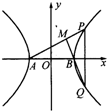 已知双曲线C:
已知双曲线C:| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
一条渐近线的方程为y=-
| ||
| 2 |
(I)求双曲线C的方程;
(Ⅱ)求直线AP与直线BQ的交点M的轨迹E的方程;
(Ⅲ)过点N(l,0)作直线l与(Ⅱ)中轨迹E交于不同两点R、S,已知点T(2,0),设
| NR |
| NS |
| TR |
| TS |
分析:(I)利用双曲线的右焦点为F(
,0),一条渐近线的方程为y=-
x,结合c2=a2+b2,可求双曲线C的方程;(Ⅱ)由A,M,P三点共线、B,M,Q三点共线,确定坐标之间的关系,利用双曲线方程,可得直线AP与直线BQ的交点M的轨迹E的方程;
(Ⅲ)①若直线l的斜率为0,不满足;
②当直线l的斜率不为0时,设方程为x=ty+1,代入
+y2=1,利用韦达定理,及
=λ
,|
+
|2=[t(y1+y2)-2]2+(y1+y2)2=16-
+
,即可求得结论.
| 3 |
| ||
| 2 |
(Ⅲ)①若直线l的斜率为0,不满足;
②当直线l的斜率不为0时,设方程为x=ty+1,代入
| x2 |
| 2 |
| NR |
| NS |
| TR |
| TS |
| 28 |
| t2+2 |
| 8 |
| (t2+2)2 |
解答:解:(I)∵双曲线的右焦点为F(
,0),一条渐近线的方程为y=-
x,
∴c=
,
=
∵c2=a2+b2,∴a=
,b=1
∴双曲线C的方程为
-y2=1;
(Ⅱ)设P(x0,y0),Q(x0,-y0),M(x,y),A(-
,0),B(
,0)
由A,M,P三点共线得:(x0+
)y=y0(x+
)
由B,M,Q三点共线得:(x0-
)y=-y0(x-
)
∴x0=
,y0=
∵
-y02=1
∴
+y2=1
∴直线AP与直线BQ的交点M的轨迹E的方程为
+y2=1(x≠0,y≠0);
(Ⅲ)①若直线l的斜率为0,则R(-
,0),S(
,0),N(1,0),
∴
=(-
-1,0),
=(
-1,0)
∴λ=-(3+2
)∉[-2,-1]
②当直线l的斜率不为0时,设方程为x=ty+1,代入
+y2=1,可得(t2+2)y2+2ty-1=0
设R(x1,y1),S(x2,y2)(y1≠0,y2≠0),则y1+y2=-
,y1y2=-
∵
=λ
,∴y1=λy2,∴λ=
,λ<0
∴λ+
+2=
+
+2=
=-
∵λ∈[-2,-1]
∴-
≤λ+
+2≤0
∴-
≤-
≤0
∴0≤t2≤
∴|
+
|2=[t(y1+y2)-2]2+(y1+y2)2=16-
+
令n=
,则n∈[
,
]
∴|
+
|2=8n2-28n+16=8(n-
)2-
∴n=
时,|
+
|2min=4;n=
时,|
+
|2max=
∴|
+
|∈[2,
].
| 3 |
| ||
| 2 |
∴c=
| 3 |
| b |
| a |
| ||
| 2 |
∵c2=a2+b2,∴a=
| 2 |
∴双曲线C的方程为
| x2 |
| 2 |
(Ⅱ)设P(x0,y0),Q(x0,-y0),M(x,y),A(-
| 2 |
| 2 |
由A,M,P三点共线得:(x0+
| 2 |
| 2 |
由B,M,Q三点共线得:(x0-
| 2 |
| 2 |
∴x0=
| 2 |
| x |
| ||
| x |
∵
| x02 |
| 2 |
∴
| x2 |
| 2 |
∴直线AP与直线BQ的交点M的轨迹E的方程为
| x2 |
| 2 |
(Ⅲ)①若直线l的斜率为0,则R(-
| 2 |
| 2 |
∴
| NR |
| 2 |
| NS |
| 2 |
∴λ=-(3+2
| 2 |
②当直线l的斜率不为0时,设方程为x=ty+1,代入
| x2 |
| 2 |
设R(x1,y1),S(x2,y2)(y1≠0,y2≠0),则y1+y2=-
| 2t |
| t2+2 |
| 1 |
| t2+2 |
∵
| NR |
| NS |
| y1 |
| y2 |
∴λ+
| 1 |
| λ |
| y1 |
| y2 |
| y2 |
| y1 |
| (y1+y2)2 |
| y1y2 |
| 4t2 |
| t2+2 |
∵λ∈[-2,-1]
∴-
| 1 |
| 2 |
| 1 |
| λ |
∴-
| 1 |
| 2 |
| 4t2 |
| t2+2 |
∴0≤t2≤
| 2 |
| 7 |
∴|
| TR |
| TS |
| 28 |
| t2+2 |
| 8 |
| (t2+2)2 |
令n=
| 1 |
| t2+2 |
| 7 |
| 16 |
| 1 |
| 2 |
∴|
| TR |
| TS |
| 7 |
| 4 |
| 17 |
| 2 |
∴n=
| 1 |
| 2 |
| TR |
| TS |
| 7 |
| 16 |
| TR |
| TS |
| 169 |
| 32 |
∴|
| TR |
| TS |
13
| ||
| 8 |
点评:本题考查双曲线的方程,考查轨迹方程,考查向量知识的运用,考查韦达定理,考查学生的计算能力,综合性强.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目