题目内容
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 过点
过点![]() ,且离心率
,且离心率![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,求
两点,求![]() 的面积的最大值.
的面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由椭圆![]() 的离心率可得出
的离心率可得出![]() ,将点
,将点![]() 的坐标代入椭圆
的坐标代入椭圆![]() 的方程,可得出
的方程,可得出![]() 和
和![]() 的值,由此可得出椭圆
的值,由此可得出椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 的方程为
的方程为![]() ,设点
,设点![]() 、
、![]() ,将直线
,将直线![]() 的方程与椭圆
的方程与椭圆![]() 的方程联立,由
的方程联立,由![]() 求出
求出![]() 的范围,列出韦达定理,利用弦长公式计算出
的范围,列出韦达定理,利用弦长公式计算出![]() ,利用点到直线的距离公式求出
,利用点到直线的距离公式求出![]() 的高,然后利用三角形的面积公式结合基本不等式可求出该三角形面积的最大值.
的高,然后利用三角形的面积公式结合基本不等式可求出该三角形面积的最大值.
(1)设椭圆![]() 的焦距为
的焦距为![]() ,则
,则![]() ,
,![]() .
.
则椭圆![]() 的方程可化为
的方程可化为![]() ,
,
将点![]() 的坐标代入椭圆
的坐标代入椭圆![]() 的方程得
的方程得![]() ,可得
,可得![]() ,
,![]() ,
,
因此,椭圆![]() 的方程为
的方程为![]() ;
;
(2)设直线![]() 的方程为
的方程为![]() ,设点
,设点![]() 、
、![]() ,
,
将直线![]() 的方程与椭圆
的方程与椭圆![]() 的方程联立
的方程联立 ,
,
消去![]() ,整理得
,整理得![]() ,
,![]() ,得
,得![]() .
.
由韦达定理得![]() ,
,![]() .
.
则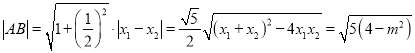 ,
,
直线![]() 的一般方程为
的一般方程为![]() ,点
,点![]() 到直线
到直线![]() 的距离为
的距离为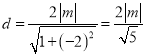 ,
,
所以,![]() ,
,
当且仅当![]() 时,即当
时,即当![]() 时,等号成立,
时,等号成立,
因此,![]() 面积的最大值为
面积的最大值为![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】微信已成为人们常用的社交软件,“微信运动”是由腾讯开发的一个类似计步数据库的公众账号.手机用户可以通过关注“微信运动”公众号查看自己每天行走的步数,同时也可以和好友进行运动量的PK或点赞.现从小明的微信朋友圈内随机选取了50人(男、女各25人),并记录了他们某一天的走路步数,并将数据整理如下表:
步数 性别 | 0~3000 | 3001~6000 | 6001~9000 | 9001~12000 | >12000 |
男 | 1 | 1 | 3 | 15 | 5 |
女 | 0 | 4 | 11 | 8 | 2 |
若某人一天走路的步数超过9000步被系统评定为“积极型”,否则被系统评定为“懈怠型”。
(1)利用样本估计总体的思想,估计小明的所有微信好友中每日走路步数超过12000步的概率;
(2)根据题意完成下面的2×2列联表,并据此判断能否有99.5%的把握认为“评定类型”与“性别”有关?
积极型 | 懈怠型 | 总计 | |
男 | |||
女 | |||
总计 |
附: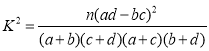 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】已知某校一间办公室有四位老师甲、乙、丙、丁.在某天的某个时段,他们每人各做一项工作,一人在查资料,一人在写教案,一人在批改作业,另一人在打印材料.
若下面4个说法都是正确的:
①甲不在查资料,也不在写教案; ②乙不在打印材料,也不在查资料;
③丙不在批改作业,也不在打印材料; ④丁不在写教案,也不在查资料.
此外还可确定:如果甲不在打印材料,那么丙不在查资料.根据以上信息可以判断
A.甲在打印材料 | B.乙在批改作业 | C.丙在写教案 | D.丁在打印材料 |
【题目】据历史记载,美日在中途岛(Midway)海战前,美方截获了日方密码电报,据美方已破译的密码得知,日方将向某岛进行军事活动,但关键含有地点的部分却被日方换成了另一种密码.经专家研究,估计是一种密匙密码,且密匙为3位.所谓密匙密码是指:将一段英文字母的明文(未加密前原文)经过对某一组数字(即密匙)的变换,改变成了另一组英文字母成为密文(加密后的文字)例如:明文:![]() (不计空格,不计大小写)在密匙为:1 9 2的条件下,变换过程如下图所示:
(不计空格,不计大小写)在密匙为:1 9 2的条件下,变换过程如下图所示:
s | t | u | d | e | n | t |
1 | 9 | 2 | 1 | 9 | 2 | 1 |
t | c | w | e | n | p | u |
则密文为:![]() ,试根据上面信息回答下面问题:
,试根据上面信息回答下面问题:
(1)在密匙为111的条件下,填写下表,并写出密文;
s | t | u | d | e | n | t |
密文____________________.
(2)若![]()
![]() 请填写下表,并写出密匙;
请填写下表,并写出密匙;
s | t | u | d | e | n | t |
密匙为_____________.
(3)若下面即是那段包含地点(Midway)的破译不出的密文:![]() ,且此段密文也是3位密匙加密,试填写下表,写出密匙,并将此段密文翻译成明文.(不必证明,写出明文即可)
,且此段密文也是3位密匙加密,试填写下表,写出密匙,并将此段密文翻译成明文.(不必证明,写出明文即可)
c | w | b | c | f | s | o | l | l | y | d | g |
密匙为___________,明文为_________.