题目内容
二次函数f(x)满足f(x)-f(x-1)=2x-2且f(0)=1.则函数y=f(x)-3的零点是________.
-1,2
分析:由题意设所求二次函数为:f(x)=ax2+bx+1,由已知可建立关于ab的方程组,解之可得f(x),进而可得y=f(x)-3的解析式,解对应的二次方程可得答案.
解答:由题意设所求二次函数为:f(x)=ax2+bx+1,
则f(x)-f(x-1)=ax2+bx+1-[a(x-1)2+b(x-1)+1]
=2ax-a+b=2x-2,所以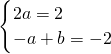 ,解得
,解得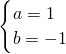 ,
,
故函数y=f(x)-3=x2-x-2,由方程x2-x-2=0解得x=-1,或x=-2,
故函数y=f(x)-3的零点是:-1,2
故答案为:-1,2
点评:本题为待定系数法求二次函数的解析式,函数的零点即对方程的根是解决问题的关键,属基础题.
分析:由题意设所求二次函数为:f(x)=ax2+bx+1,由已知可建立关于ab的方程组,解之可得f(x),进而可得y=f(x)-3的解析式,解对应的二次方程可得答案.
解答:由题意设所求二次函数为:f(x)=ax2+bx+1,
则f(x)-f(x-1)=ax2+bx+1-[a(x-1)2+b(x-1)+1]
=2ax-a+b=2x-2,所以
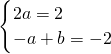 ,解得
,解得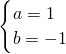 ,
,故函数y=f(x)-3=x2-x-2,由方程x2-x-2=0解得x=-1,或x=-2,
故函数y=f(x)-3的零点是:-1,2
故答案为:-1,2
点评:本题为待定系数法求二次函数的解析式,函数的零点即对方程的根是解决问题的关键,属基础题.

练习册系列答案
相关题目