��Ŀ����
����С������12�֣�
ij��Ϊ�˶�ѧ������������ѧ��������ѧϰ�������з�������10000��ѧ����������100λѧ���������ۺ�ѧϰ�����ȼ�����(6����)��Ϊ����������Ƶ���ֲ����±���
| �ȼ��÷� |  | 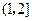 |  |  | 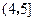 |  |
| ���� | 3 | 17 | 30 | 30 | 17 | 3 |
����ͳ�Ʒ����У�ͬһ�����ݳ��ø���������е�ֵ����������
 ���е�ֵΪ1.5����Ϊ������
���е�ֵΪ1.5����Ϊ������(��)�ݴˣ�������100��ѧ������ѧϰ������
 ������������
������������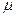 ������
������ (��ȷ��0.1)��
(��ȷ��0.1)��(��) �����������̬�ֲ�,��������������,���Ƹ�����10000��ѧ��������ѧϰ�����ȼ���
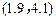 ��Χ�ڵ����� ��
��Χ�ڵ����� ��������10000��ѧ���������ȡ5��ͬѧ��
������ѧ����������ѧϰ�����ȼ���
�����±���


�������뻭���ϱ����ݵ�ɢ��ͼ��
������������ϱ��ṩ�����ݣ�����С���˷����
 ����
���� �����Իع鷽��
�����Իع鷽��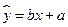 �����ο����ݣ�
�����ο����ݣ�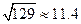 ��
��
�⣺���������У�ѧ��Ϊ���õ�����Ϊ�����ˣ��ʴ������������ȡ ����ѧ��������У���ѧ��Ϊ���õĸ���Ϊ
����ѧ��������У���ѧ��Ϊ���õĸ���Ϊ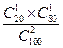 ��
��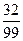 -------------2��
-------------2��
���� (��)�������ݵ����� ԼΪ��
ԼΪ��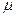 =0.5��0.03+1.5��0.17+2.5��0.30+3.5��0.30+4.5��0.17+5.5��0.03=3.0-------------4��
=0.5��0.03+1.5��0.17+2.5��0.30+3.5��0.30+4.5��0.17+5.5��0.03=3.0-------------4��
���� =
=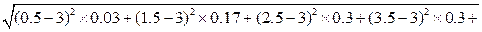
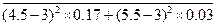 ��
��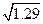
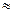 1.1---------------6��
1.1---------------6��
(��)����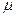 ="3,"
="3," 
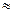 1
1 .1
.1
��x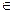
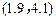 ʱ����x
ʱ����x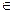 (
(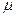 -
- ,
,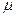 +
+ )
)
����ѧѧϰ�����ȼ�������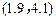 ��Χ�еĸ���0.6826��
��Χ�еĸ���0.6826��
��ѧѧϰ�����ȼ���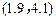 ��Χ�е�ѧ��������ԼΪ6826�ˣ�-----------------8��
��Χ�е�ѧ��������ԼΪ6826�ˣ�-----------------8��
����
���������ݵ�ɢ��ͼ����ͼ��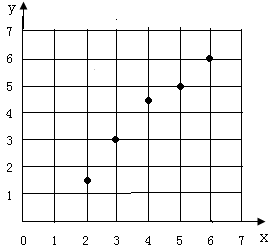
-------------9��
�����������Իع鷽��Ϊ ����
����
����һ: 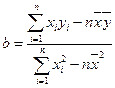 =
=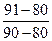 ="1.1 "
="1.1 "  =4��1.1��4=-0.4
=4��1.1��4=-0.4
�ʻع�ֱ�߷���Ϊ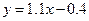 -----12��
-----12��
������: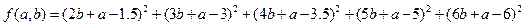

�� ʱ��
ʱ��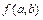 ȡ����Сֵ10b
ȡ����Сֵ10b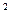 -22b+12.5
-22b+12.5
������ ʱ�棨a���⣩ȡ����Сֵ��
ʱ�棨a���⣩ȡ����Сֵ��
�������Իع鷽��Ϊ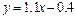 .---------12��
.---------12��
����

��ϰ��ϵ�д�
 ��ǰ����ϵ�д�
��ǰ����ϵ�д�
�����Ŀ